题目内容
 如图所示,物体A放存固定的斜面B上,在A上施加一个竖直向下的恒力F,下列说法中正确的有( )
如图所示,物体A放存固定的斜面B上,在A上施加一个竖直向下的恒力F,下列说法中正确的有( )| A、若A原来是静止的,则施加力F后,A将加速下滑 | B、若A原来是静止的,则施加力F后,A仍保持静止 | C、若A原来是加速下滑的,则施加力F后,A的加速度不变 | D、若A原来是加速下滑的,则施加力F后,A的加速度将增大 |
分析:分别对未加外力和加外力时物体A进行受力分析,A原来静止看成恰好静止进行分析,判断A物体是否静止.当A原来加速下滑,根据牛顿第二定律判断加速度的变化.
解答:解:AB、若A原来静止,有:mgsinα≤μmgcosα,施加F后,因为仍有(F+mg)sinα≤μ(F+mg)cosα,则A仍然保持静止.故B正确,A错误.
CD、未加F时,物体受重力、支持力和摩擦力,根据牛顿第二定律有:a=
,当施加F后,加速度a′=
,因为gsinα>μgcosα,所以Fsinα>μFcosα,可见a′>a,即加速度增大.故C错误,D正确.
故选:BD.
CD、未加F时,物体受重力、支持力和摩擦力,根据牛顿第二定律有:a=
| mgsinθ-μmgcosθ |
| m |
| (mg+F)sinθ-μ(F+mg)cosθ |
| m |
故选:BD.
点评:解决本题的关键能够正确地进行受力分析,运用牛顿第二定律进行求解.

练习册系列答案
相关题目
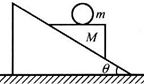 如图所示,一个劈形物体M放存固定的粗糙斜面上,其上面呈水平.在其水平面上放一光滑小球m.当劈形物体从静止开始释放后,观察到m和M有相对运动,则小球m在碰到斜面前的运动轨迹是( )
如图所示,一个劈形物体M放存固定的粗糙斜面上,其上面呈水平.在其水平面上放一光滑小球m.当劈形物体从静止开始释放后,观察到m和M有相对运动,则小球m在碰到斜面前的运动轨迹是( )
