题目内容
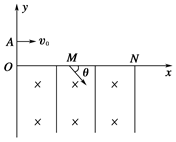
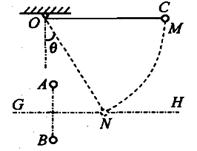
分如图所示,直角坐标系xOy位于竖直平面内,在水平的x轴下方存在匀强磁场和匀强电场,磁场的磁感应强度为B,方向垂直xOy平面向里,电场线平行于y轴.一质量为m、电荷量为q的带正电荷的小球,从y轴上的A点水平向右抛出.经x轴上的M点进入电场和磁场,恰能做匀速圆周运动,从x轴上的N点第一次离开电场和磁场,MN之间的距离为L,小球过M点时的速度方向与x轴正方向夹角为θ.不计空气阻力,重力加速度为g,求:
(1)电场强度E的大小和方向;
(2)小球从A点抛出时初速度v0的大小;
(3)A点到x轴的高度h.

(1)电场强度E的大小和方向;
(2)小球从A点抛出时初速度v0的大小;
(3)A点到x轴的高度h.
(1)E=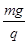 ,竖直向上(4分) (2)
,竖直向上(4分) (2)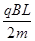 cotθ(6分) (3)
cotθ(6分) (3)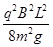
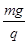 ,竖直向上(4分) (2)
,竖直向上(4分) (2)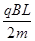 cotθ(6分) (3)
cotθ(6分) (3)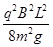
试题分析:(1)小球在电场、磁场中恰能做匀速圆周运动,其所受电场力必须与重力平衡,
有qE=mg ①
E=
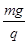 ②
② 重力的方向是竖直向下,电场力的方向则应为竖直向上,由于小球带正电,所以电场强度方向竖直向上.
(2)小球做匀速圆周运动,O′为圆心,MN为弦长,∠MO′P=θ,如图所示.
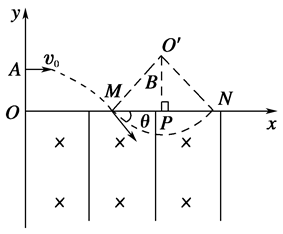
设半径为r,由几何关系知
 =sinθ③
=sinθ③小球做匀速圆周运动的向心力由洛伦兹力提供,设小球做圆周运动的速率为v,
有qvB=
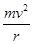 ④
④由速度的合成与分解知
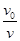 =cosθ⑤
=cosθ⑤由③④⑤式得v0=
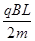 cotθ⑥
cotθ⑥(3)设小球到M点时的竖直分速度为vy,它与水平分速度的关系为vy=v0tanθ⑦
由匀变速直线运动规律v
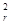 =2gh⑧
=2gh⑧由⑥⑦⑧式得h=
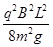 ⑨
⑨点评:难度较大,处理带电粒子在交替复合场中的运动时,应分割整个过程,判断各个分过程的受力和运动情况,画出大致的运动轨迹,本题中进入第四象限做匀速圆周运动,肯定是电场力平衡重力,由洛伦兹力提供向心力

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
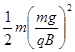
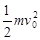



 ,求:
,求: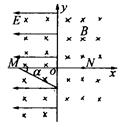
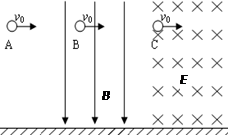
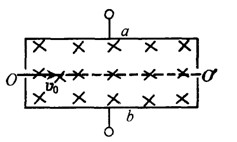
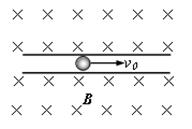
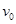 经小孔进入正交电磁场可沿直线
经小孔进入正交电磁场可沿直线 运动,由
运动,由 射出,粒子所受重力不计,则a板所带电量情况是
射出,粒子所受重力不计,则a板所带电量情况是