题目内容
3.甲、乙两颗人造地球卫星沿不同轨道绕地球做圆周运动,两卫星的轨道半径分别为r甲和r乙,已知r甲>r乙.若甲、乙两卫星线速度分别为v甲和v乙,周期分别为T甲和T乙,则( )| A. | v甲<v乙,T甲>T乙 | B. | v甲<v乙,T甲<T乙 | C. | v甲>v乙,T甲>T乙 | D. | v甲>v乙,T甲<T乙 |
分析 根据人造卫星的万有引力等于向心力,列式求出线速度、角速度、周期和向心力的表达式进行讨论即可.
解答 解:人造卫星绕地球做匀速圆周运动,根据万有引力提供向心力,
设卫星的质量为m、轨道半径为r、地球质量为M,有F引=F向 即$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$
解得v=$\sqrt{\frac{GM}{r}}$ 因为r甲>r乙,所以v甲<v乙 ;
$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}r$
解得$T=2π\sqrt{\frac{{r}^{3}}{GM}}$
因为r甲>r乙,所以T甲>T乙 ;
故选:A
点评 本题关键抓住万有引力提供向心力,列式求解出线速度、角速度、周期和向心力的表达式,再进行讨论.

练习册系列答案
相关题目
19. 地球表面的磁场形状如图所示,若在我们的教室中(北京地区)让一个质子由西向东做直线运动,在运动过程中该质子会受到地磁场所施加的洛仑兹力f.那么( )
地球表面的磁场形状如图所示,若在我们的教室中(北京地区)让一个质子由西向东做直线运动,在运动过程中该质子会受到地磁场所施加的洛仑兹力f.那么( )
 地球表面的磁场形状如图所示,若在我们的教室中(北京地区)让一个质子由西向东做直线运动,在运动过程中该质子会受到地磁场所施加的洛仑兹力f.那么( )
地球表面的磁场形状如图所示,若在我们的教室中(北京地区)让一个质子由西向东做直线运动,在运动过程中该质子会受到地磁场所施加的洛仑兹力f.那么( )| A. | f的竖直方向的分力向下 | B. | f的水平方向的分力大致向东 | ||
| C. | f的水平方向的分力大致向北 | D. | f的水平方向的分力大致向南 |
20. 从某一地点同时开始沿同一方向做直线运动的两个物体 I、II,其v-t图象如图所示.在0~t0时间内下列说法中正确的是( )
从某一地点同时开始沿同一方向做直线运动的两个物体 I、II,其v-t图象如图所示.在0~t0时间内下列说法中正确的是( )
 从某一地点同时开始沿同一方向做直线运动的两个物体 I、II,其v-t图象如图所示.在0~t0时间内下列说法中正确的是( )
从某一地点同时开始沿同一方向做直线运动的两个物体 I、II,其v-t图象如图所示.在0~t0时间内下列说法中正确的是( )| A. | 两个物体Ⅰ、Ⅱ所受合外力都在不断减小 | |
| B. | 物体Ⅰ所受合外力不断增大,物体Ⅱ所受合外力不断减小 | |
| C. | 物体Ⅰ的位移不断增大,物体Ⅱ的位移不断减小 | |
| D. | 两物体Ⅰ、Ⅱ的平均速度大小都是$\frac{{v}_{1}+{v}_{2}}{2}$ |
17. 如图所示,初速为零的电子经电压U1加速后,垂直进入偏转电场偏转,离开偏转电场时侧向位移是h.偏转板间距离为d,偏转电压为U2,板长为l.为了提高偏转灵敏度(每单位偏转电压引起的侧向位移),可采用( )
如图所示,初速为零的电子经电压U1加速后,垂直进入偏转电场偏转,离开偏转电场时侧向位移是h.偏转板间距离为d,偏转电压为U2,板长为l.为了提高偏转灵敏度(每单位偏转电压引起的侧向位移),可采用( )
 如图所示,初速为零的电子经电压U1加速后,垂直进入偏转电场偏转,离开偏转电场时侧向位移是h.偏转板间距离为d,偏转电压为U2,板长为l.为了提高偏转灵敏度(每单位偏转电压引起的侧向位移),可采用( )
如图所示,初速为零的电子经电压U1加速后,垂直进入偏转电场偏转,离开偏转电场时侧向位移是h.偏转板间距离为d,偏转电压为U2,板长为l.为了提高偏转灵敏度(每单位偏转电压引起的侧向位移),可采用( )| A. | 增大两板间电势差U2 | B. | 尽可能使板长l短一些 | ||
| C. | 尽可能使板距d小一些 | D. | 使加速电压U1升高一些 |
4.假设我国发射的探月卫星“嫦娥一号”的绕月运行轨道和载人飞船“神舟七号”的绕地运动轨道都可以看成是圆轨道,且不计卫星到月球表面的距离和飞船到地球表面的距离.已知月球质量约为地球质量的$\frac{1}{81}$,月球半径约为地球半径的$\frac{1}{4}$,地球上的第一宇宙速度约为7.9m/s,卫星和飞船的轨道半径为别为r星和r船,周期分别为T星和T船,且K星=$\frac{{r}_{星}^{3}}{{T}_{星}^{2}}$,K船=$\frac{{r}_{船}^{3}}{{T}_{船}^{2}}$.则下列说法或结果正确的是( )
| A. | 神舟七号绕地运行的速率大于7.9km/s | |
| B. | 嫦娥一号绕月运行的速率为3.95km/s | |
| C. | K星:K船=1:81 | |
| D. | T星:T船=1:4 |
15.关于磁通量,下列说法正确的是( )
| A. | 磁通量越大,磁感应强度越大 | |
| B. | 磁通量不仅有大小而且有方向,所以是矢量 | |
| C. | 磁感应强度就是磁通密度 | |
| D. | 穿过某一面积的磁通量为零,该处的磁感应强度不一定为零 |
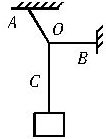 如图所示,三段不可伸长的细绳OA、OB、OC能承受的最大拉力相同,它们共同悬挂一重物.其中细绳OB是水平的,A端、B端固定.若逐渐增加C端所挂物体的质量,试判断那段绳子先断?
如图所示,三段不可伸长的细绳OA、OB、OC能承受的最大拉力相同,它们共同悬挂一重物.其中细绳OB是水平的,A端、B端固定.若逐渐增加C端所挂物体的质量,试判断那段绳子先断?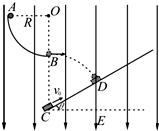 如图所示,在竖直平面内固定一光滑$\frac{1}{4}$圆弧轨道AB,轨道半径为R=0.4m,轨道最高点A与圆心O等高.有一倾角θ=30°的斜面,斜面底端C点在圆弧轨道B点正下方.圆弧轨道和斜面均处于场强E=100N/C、竖直向下的匀强电场中.现将一个质量为m=0.02kg、带电量为q=+2×10-3C的带点小球从A点静止释放,小球通过B点离开圆弧轨道沿水平方向飞出,当小球运动到斜面上D点时速度方向恰与斜面垂直,并刚好与一个以一定初速度从斜面底端上滑的物块相遇.若物块与斜面间动摩擦因数μ=$\frac{\sqrt{3}}{5}$,空气阻力不计,g取10m/s2,小球和物块都可视为质点.求:
如图所示,在竖直平面内固定一光滑$\frac{1}{4}$圆弧轨道AB,轨道半径为R=0.4m,轨道最高点A与圆心O等高.有一倾角θ=30°的斜面,斜面底端C点在圆弧轨道B点正下方.圆弧轨道和斜面均处于场强E=100N/C、竖直向下的匀强电场中.现将一个质量为m=0.02kg、带电量为q=+2×10-3C的带点小球从A点静止释放,小球通过B点离开圆弧轨道沿水平方向飞出,当小球运动到斜面上D点时速度方向恰与斜面垂直,并刚好与一个以一定初速度从斜面底端上滑的物块相遇.若物块与斜面间动摩擦因数μ=$\frac{\sqrt{3}}{5}$,空气阻力不计,g取10m/s2,小球和物块都可视为质点.求: