Question

【题目】开普勒第三定律指出：所有行星轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等，即，其中a表示椭圆轨道半长轴，T表示公转周期，比值c是一个对所有行星都相同的常量。牛顿把该定律推广到宇宙中一切物体之间，提出了万有引力定律：

(1)开普勒第三定律对于轨迹为圆形和直线的运动依然适用。圆形轨迹可以认为中心天体在圆心处，半长轴为轨迹半径。直线轨迹可以看成无限扁的椭圆轨迹，此时中心天体在轨迹端点，半长轴为轨迹长度的。已知：某可视为质点的星球质量为M，引力常量为G。一物体与星球的距离为r。该物体在星球引力作用下运动，其他作用力忽略不计。

a.若物体绕星球作匀速圆周运动，请你推导该星球的引力系统中常量c的表达式；

b.若物体由静止开始做直线运动。求物体到达星球所经历的时间；

(2)万有引力和静电引力是自然界中典型的两种引力，库仑定律和万有引力定律均遵循“平方反比”规律，类比可知，带电粒子在电场中的运动也遵循开普勒第三定律。两个点电荷带电量分别为+Q和－Q，质量均为m，从相距为2l的两点由静止释放，在静电引力的作用下运动，其他作用力忽略不计。静电力常量为k。求两点电荷从开始释放到相遇的时间。

Answer 1

【答案】(1)a.；b. ；(2)

【解析】

(1)a.设物体质量为m0，则

解得

b.把直线运动看成是很扁的椭圆运动，设物体到达星球经历的时间为t，则物体的周期为2t，半长轴为，则

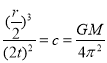
解得

(2)两个点电荷由静止开始做变加速直线运动，将在中点O点相遇。对于电荷+Q，它所受到的静电引力相当于O点固定一个电荷量为q的点电荷对它的引力。电荷+Q到O点距离为l。则

解得

设电荷+Q绕q作半径为l的匀速圆周运动时周期为T1，类比可得该引力系统中的常量c1，即

解得

设两点电荷从开始运动到相遇的时间为t1，把+Q向O点的直线运动看成是很扁的椭圆运动，半长轴为，周期为2t1.则

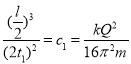
解得