题目内容
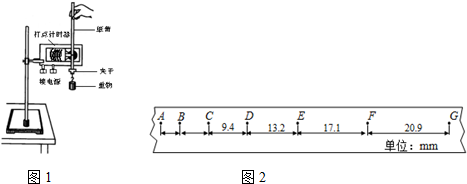
11. 质量为m=2.0kg的物体,从竖直平面内高h=0.45m的光滑弧形轨道上的A点,无初速地沿轨道滑下,并进入水平轨道BC,如图所示.已知物体与水平轨道间的动摩擦因数μ=0.40,求:
质量为m=2.0kg的物体,从竖直平面内高h=0.45m的光滑弧形轨道上的A点,无初速地沿轨道滑下,并进入水平轨道BC,如图所示.已知物体与水平轨道间的动摩擦因数μ=0.40,求:(1)物体滑至B点时速度的大小;
(2)物体在水平轨道上受到的滑动摩擦力的大小;
(3)物体最后停止在离B点多远的位置上.
分析 (1)物体从A滑到B点过程中,应用动能定理可以求出物体在B点的速度.
(2)应用滑动摩擦力公式可以求出滑动摩擦力大小;
(3)对整个过程,应用动能定理可以求出物体停下时与B点间的距离
解答 解:(1)物体从弧形轨道下滑过程中,
由动能定理可得:mgh=$\frac{1}{2}$mv2-0,
解得:v=$\sqrt{2gh}$=$\sqrt{2×10×0.45}$=3m/s;
(2)滑动摩擦力:f=μmg=0.4×2×10=8N;
(3)在整个运动过程中,
由动能定理可得:mgh-μmgx=0-0,
即:2×10×0.45-0.4×2×10x=0-0,
解得:x=1.125m;
答:(1)物体滑至B点时的速度为3m/s.
(2)物体在水平轨道上受到的滑动摩擦力的大小为8N.
(2)物体最后停止在离B点1.125m的位置上.
点评 本题考查了动能定理的应用,只要熟练应用动能定理即可正确解题,本题难度不大;本题最后一问也可以应用牛顿第二定律与运动学公式解题.

练习册系列答案
相关题目
6.质量为m,带+q电量的物块静止在绝缘水平面上.在空间加上竖直向上的匀强电场,经时间t撤去电场,物块又经过时间t回到出发点,此时物体的动能为Ek.不计空气阻力,重力加速度大小为g则下列说法正确的是( )
| A. | 撤去电场前后物块的加速度大小之比为1:3 | |
| B. | 电场强度大小为$\frac{2mg}{q}$ | |
| C. | 撤去电场时,物物块的重力势能是$\frac{1}{2}$Ek | |
| D. | 撤去电场时,物块的动能是$\frac{1}{4}$Ek |
16.“神九”载人飞船与天宫一号成功对接和“蛟龙”号下潜突破7000米,双双入围2012年中国十大科技进展新闻.假设地球是一半径为R、质量分布均匀的球体.已知质量分布均匀的球壳对壳内物体的引力为零.若“蛟龙”下潜深度为d,天宫一号轨道距离地面高度为h,则“蛟龙”号所在处与“天宫一号”所在处的重力加速度大小之比为( )
| A. | $\frac{R-d}{R+h}$ | B. | $\frac{(R-d)^{2}}{(R+h)^{2}}$ | C. | $\frac{(R-d)(R+h)}{{R}^{2}}$ | D. | $\frac{(R-d)(R+h)^{2}}{{R}^{3}}$ |
20.以下涉及物理学史上的四个重大发现,其中说法不正确的是( )
| A. | 卡文迪许通过扭秤实验,测定出了万有引力恒量 | |
| B. | 奥斯特通过实验研究,发现了电流周围存在磁场 | |
| C. | 安培通过实验研究,总结出电磁感应定律 | |
| D. | 牛顿根据理想斜面实验,提出力不是维持物体运动的原因 |
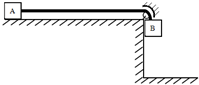 如图,A、B两物体通过一柔软且不可伸长的绳子连接,跨在光滑小滑轮两侧,软绳与水平接触面平行,已知A、B两物体的质量均为m,且可视为质点,软绳质量也为m,长为2L,平台离地高L,不计运动过程中的一切摩擦,刚开始软绳全部在水平面内,现无初速释放B,A、B在重力作用下开始运动,若B触地后不再反弹.求:
如图,A、B两物体通过一柔软且不可伸长的绳子连接,跨在光滑小滑轮两侧,软绳与水平接触面平行,已知A、B两物体的质量均为m,且可视为质点,软绳质量也为m,长为2L,平台离地高L,不计运动过程中的一切摩擦,刚开始软绳全部在水平面内,现无初速释放B,A、B在重力作用下开始运动,若B触地后不再反弹.求: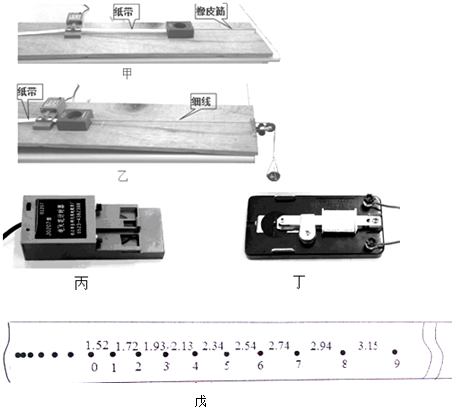
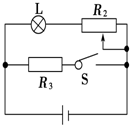 如图所示,R3=6Ω,电源电动势E=8V,内阻r=1Ω,当S闭合时,标有“4V,4W”的灯泡L正常发光,求:
如图所示,R3=6Ω,电源电动势E=8V,内阻r=1Ω,当S闭合时,标有“4V,4W”的灯泡L正常发光,求: 如图所示,质量M=8kg的小车放在水平光滑的平面上,在小车左端加一水平推力F=8N,当小车向右运动的速度达到1.5m/s时,在小车前端轻轻地放上一个大小不计,质量为m=2kg的小物块,物块与小车间的动摩擦因数μ=0.2,小车足够长.求:
如图所示,质量M=8kg的小车放在水平光滑的平面上,在小车左端加一水平推力F=8N,当小车向右运动的速度达到1.5m/s时,在小车前端轻轻地放上一个大小不计,质量为m=2kg的小物块,物块与小车间的动摩擦因数μ=0.2,小车足够长.求: