题目内容
如图所示,圆心在原点、半径为R的圆将xOy平面分为两个区域,在圆内区域Ⅰ(r≤R)和圆外区域Ⅱ(r>R)分别存在两个磁场方向均垂直于XOY平面的匀强磁场;垂直于XOY平面放置了两块平面荧光屏,其中荧光屏甲平行于X轴放置在Y轴坐标为-2.22R的位置,荧光屏乙平行于Y轴放置在X轴坐标为3.5R的位置。现有一束质量为m、电荷量为q(q>0)、动能为E0的粒子从坐标为(-R,0)的A点沿X轴正方向射入区域Ⅰ,最终打在荧光屏甲上,出现坐标为(0.4R, -2.2R,)的亮点 。若撤去圆外磁场,粒子打在荧光屏甲上,出现坐标为(0,-2.2R)的亮点M。此时,若将荧光屏甲沿Y轴负方向平移,则亮点的X轴坐标始终保持不变。(不计粒子重力影响)
。若撤去圆外磁场,粒子打在荧光屏甲上,出现坐标为(0,-2.2R)的亮点M。此时,若将荧光屏甲沿Y轴负方向平移,则亮点的X轴坐标始终保持不变。(不计粒子重力影响)

(1)求在区域Ⅰ和Ⅱ中粒子运动速度v1、v2 的大小。
(2)求在区域Ⅰ和Ⅱ中磁感应强度B1、B2的大小和方向。
(3)若上述两个磁场保持不变,荧光屏仍在初始位置,但从A点沿X轴正方向射入区域Ⅰ的粒子束改为质量为m、电荷量为-q、动能为3E0的粒子,求荧光屏上的亮点的位置。
 。若撤去圆外磁场,粒子打在荧光屏甲上,出现坐标为(0,-2.2R)的亮点M。此时,若将荧光屏甲沿Y轴负方向平移,则亮点的X轴坐标始终保持不变。(不计粒子重力影响)
。若撤去圆外磁场,粒子打在荧光屏甲上,出现坐标为(0,-2.2R)的亮点M。此时,若将荧光屏甲沿Y轴负方向平移,则亮点的X轴坐标始终保持不变。(不计粒子重力影响)
(1)求在区域Ⅰ和Ⅱ中粒子运动速度v1、v2 的大小。
(2)求在区域Ⅰ和Ⅱ中磁感应强度B1、B2的大小和方向。
(3)若上述两个磁场保持不变,荧光屏仍在初始位置,但从A点沿X轴正方向射入区域Ⅰ的粒子束改为质量为m、电荷量为-q、动能为3E0的粒子,求荧光屏上的亮点的位置。
试题分析:(1)由于在磁场中运动时洛仑兹力不做功,所以在区域Ⅰ和Ⅱ中粒子运动速度大小就是在
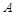 点入射时初始速度大小
点入射时初始速度大小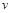 ,由
,由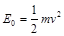 可得
可得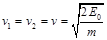 ① (2分)
① (2分)(1)粒子在区域Ⅰ中运动了四分之一圆周后,从
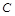 点沿
点沿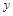 轴负方向进入区域Ⅱ的磁场
轴负方向进入区域Ⅱ的磁场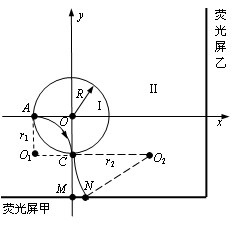
如图所示,圆周运动的圆心是
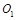 点,半径为
点,半径为(1)
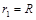 ② (2分)
② (2分)由
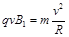 可得
可得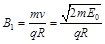 ③ (2分)
③ (2分)方向垂直
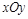 平面向外。 ④ (1分)
平面向外。 ④ (1分)粒子进入区域Ⅱ后做半径为
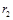 的圆周运动,由
的圆周运动,由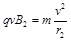
可得
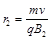 ⑤
⑤圆周运动的圆心
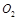 坐标为(
坐标为(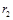 ,
,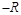 ),圆周运动轨迹方程为
),圆周运动轨迹方程为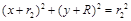
将
 点的坐标(
点的坐标( ,
,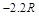 )代入上式,可得
)代入上式,可得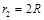 ⑥ (2分)
⑥ (2分)利用⑤、⑥式得
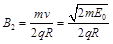 ⑦ (2分)
⑦ (2分)方向垂直
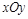 平面向里。 ⑧ (1分)
平面向里。 ⑧ (1分)(3)
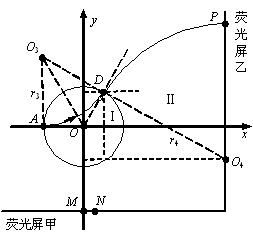
如图所示,粒子先在区域Ⅰ中做圆周运动。由
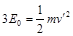 可知,运动速度为
可知,运动速度为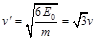 类似于⑤式,半径为
类似于⑤式,半径为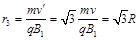 ⑨ (2分)
⑨ (2分)由圆心
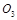 的坐标(
的坐标(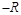 ,
,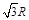 )可知,
)可知,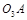 与
与 的夹角为
的夹角为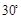 。通过分析如图的几何关系,粒子从
。通过分析如图的几何关系,粒子从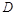 点穿出区域Ⅰ的速度方向与
点穿出区域Ⅰ的速度方向与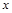 轴正方向的夹角为
轴正方向的夹角为 ⑩ (3分)
⑩ (3分)粒子进入区域Ⅱ后做圆周运动的半径为
 (2分)
(2分)其圆心
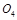 的坐标为(
的坐标为( ,
, ),即(
),即(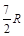 ,
,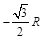 ),说明圆心
),说明圆心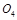 恰好在荧光屏乙上。所以,亮点将出现在荧光屏乙上的
恰好在荧光屏乙上。所以,亮点将出现在荧光屏乙上的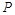 点,其
点,其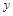 轴坐标为
轴坐标为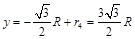 (3分)
(3分)点评:根据粒子的坐标,定出圆心,并画出运动轨道,由几何关系来确定半径,从而求出磁感应强度大小及判定其方向.值得注意的是:磁场方向相反时粒子运动圆弧所对应的圆心在一条直线上.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




 时,求此时杆的加速度大小;
时,求此时杆的加速度大小;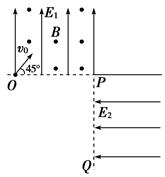
 圆弧。一个质量为m电荷量为q的带负电小球,从A点正上方高为H处由静止释放,并从A点沿切线进入半圆轨道。不计空气阻力及一切能量损失,关于带电粒子的运动情况,下列说法错误的是( )
圆弧。一个质量为m电荷量为q的带负电小球,从A点正上方高为H处由静止释放,并从A点沿切线进入半圆轨道。不计空气阻力及一切能量损失,关于带电粒子的运动情况,下列说法错误的是( )

 的竖直匀强电场中,有一光滑的半圆形绝缘轨QPN与一水平绝缘轨道MN连接,半圆形轨道平面与电场线平行,P为QN圆弧的中点,其半径R=40cm,一带正电q=10-4C的小滑块质量m=10g,与水平轨道间的动摩擦因数
的竖直匀强电场中,有一光滑的半圆形绝缘轨QPN与一水平绝缘轨道MN连接,半圆形轨道平面与电场线平行,P为QN圆弧的中点,其半径R=40cm,一带正电q=10-4C的小滑块质量m=10g,与水平轨道间的动摩擦因数 ,位于N点右侧x=1.5m处,取g=10m/s2,求:
,位于N点右侧x=1.5m处,取g=10m/s2,求: