题目内容
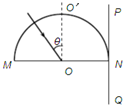 固定的半圆形玻璃砖的横截面如图.O点为圆心,OO′为直径MN的垂线.足够大的光屏PQ紧靠玻瑞砖右侧且垂直于MN.由A、B两种单色光组成的一束光沿半径方向射向O点,入射光线与OO′夹角θ较小时,光屏NQ区域出现两个光斑?逐渐增大θ角.当θ=α时,光屏NQ区城A光的光斑消失,继续增大θ角,当θ=β时,光屏NQ区域B光的光斑消失,则.
固定的半圆形玻璃砖的横截面如图.O点为圆心,OO′为直径MN的垂线.足够大的光屏PQ紧靠玻瑞砖右侧且垂直于MN.由A、B两种单色光组成的一束光沿半径方向射向O点,入射光线与OO′夹角θ较小时,光屏NQ区域出现两个光斑?逐渐增大θ角.当θ=α时,光屏NQ区城A光的光斑消失,继续增大θ角,当θ=β时,光屏NQ区域B光的光斑消失,则.分析:由题,当光斑在光屏上消失时,是由于光线发生了全反射,A光先消失,说明A光的临界角较小,根据临界角公式sinC=
,即可确定玻璃对两种光折射率的大小;由v=
,判断光在玻璃中传播速度的大小;对照全反射的条件,当光线从玻璃射入空气,入射光大于临界角时光线将发生全反射进行分析.
| 1 |
| n |
| c |
| n |
解答:解:A、根据题干描述“当θ=α时,光屏NQ区域A光的光斑消失,继续增大θ角,当θ=β时,光屏NQ区域B光的光斑消失”,说明A光先发生了全反射,A光的临界角小于B光的临界角,而发生全反射的临界角C满足:sinC=
,可知,玻璃砖对A光的折射率比对B光的大,故A正确;
B、玻璃砖对A光的折射率比对B光的大,由n=
知,A光在玻璃砖中传播速度比B光的小.故B错误.
C、当α<θ<β 时,B光尚未发生全反射现象,故光屏上应该看到2个亮斑,其中包含NP侧的反射光斑(A、B重合)以及NQ一侧的B光的折射光线形成的光斑.故C错误.
D、当β<θ<
π时,A、B两光均发生了全反射,故仅能看到NP侧的反射光斑(A、B重合).故D正确.
故选AD
| 1 |
| n |
B、玻璃砖对A光的折射率比对B光的大,由n=
| c |
| n |
C、当α<θ<β 时,B光尚未发生全反射现象,故光屏上应该看到2个亮斑,其中包含NP侧的反射光斑(A、B重合)以及NQ一侧的B光的折射光线形成的光斑.故C错误.
D、当β<θ<
| 1 |
| 2 |
故选AD
点评:本题主要考察几何光学和物理光学的基础知识应用,关键要掌握全反射的条件及临界角公式进行分析.

练习册系列答案
相关题目
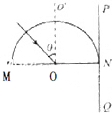 固定的半圆形玻璃砖的横截面如图.O点为圆心,OO′为直径MN的垂线.足够大的光屏PQ紧靠玻瑞砖右侧且垂直于MN.由A、B两种单色光组成的一束光沿半径方向射向O点,入射光线与OO′夹角θ较小时,光屏NQ区城出现两个光斑?逐渐增大θ角.当θ=α时,光屏NQ区城A光的光斑消失,继续增大θ角,当θ=β时,光屏NQ区域B光的光斑消失,则( )
固定的半圆形玻璃砖的横截面如图.O点为圆心,OO′为直径MN的垂线.足够大的光屏PQ紧靠玻瑞砖右侧且垂直于MN.由A、B两种单色光组成的一束光沿半径方向射向O点,入射光线与OO′夹角θ较小时,光屏NQ区城出现两个光斑?逐渐增大θ角.当θ=α时,光屏NQ区城A光的光斑消失,继续增大θ角,当θ=β时,光屏NQ区域B光的光斑消失,则( )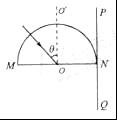

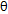 角,当θ=β时,光屛NQ区域B光的光斑消失,则( )
角,当θ=β时,光屛NQ区域B光的光斑消失,则( )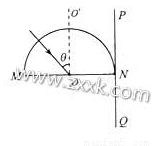
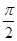 时,光屛上只有1个光斑
时,光屛上只有1个光斑 (1+
(1+ sin2
sin2 ).为了用图象法验证单摆周期T和最大摆角θ的关系,他测出摆长为l的同一单摆在不同最大摆角θ时的周期T,并根据实验数据描绘出如图乙所示的图线.根据周期公式可知,图乙中的纵轴表示的是______,图线延长后与横轴交点的横坐标为______
).为了用图象法验证单摆周期T和最大摆角θ的关系,他测出摆长为l的同一单摆在不同最大摆角θ时的周期T,并根据实验数据描绘出如图乙所示的图线.根据周期公式可知,图乙中的纵轴表示的是______,图线延长后与横轴交点的横坐标为______