Question

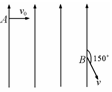
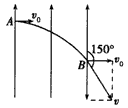
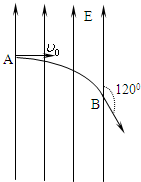如图所示，电子以v₀的速度沿与电场垂直的方向从A点飞入匀强电场，并且从另一端B点沿与场强方向成120°角的方向飞出，设电子的电量为e，质量为m，求A、B两点间的电势差U_AB是多少？（不计电子的重力）

Answer 1

分析：电子垂直进入匀强电场中，做类平抛运动，作出电子经过B点时速度的分解图，求出经过B点时的速度，根据动能定理求解A、B两点间的电势差

解答：解：从A到B过程，由动能定理得：-eU=

1

2

mv2-

1

2

m

v

2 0

又因为：cos30°=

v0

v

=

3

2

所以：U=-

m v 2 0

6e

答：A、B两点间的电势差是U=-

m v 2 0

6e

点评：本题运用动能定理求电势差，也可以根据类平抛运动的特点，牛顿第二定律和运动学结合求解．