题目内容
8.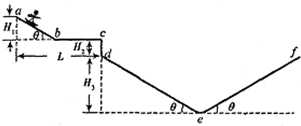 滑板运动是一项陆地上的“冲浪运动”,具有很强的观赏性.如图所示,abcdef为同一竖直平面内的滑行轨道,其中bc段水平,ab、dc和ef均为倾角θ=37°的斜直轨道,轨道间均用小圆弧平滑相连(小圆弧的长度可忽略).已知H1=5m,L=15m,H2=1.25m,H3=12.75m,设滑板与轨道之间的摩擦力为它们间压力的k倍(k=0.25),运动员连同滑板的总质量m=60kg.运动员从a点由静止开始下滑从c点水平飞出,在de上着陆后,经短暂的缓冲动作后只保留沿斜面方向的分速度下滑,接着在def轨道上来回滑行,除缓冲外运动员连同滑板可视为质点,忽略空气阻力,取g=l0m/s2,sin37°=06,cos37°=0.8.求:
滑板运动是一项陆地上的“冲浪运动”,具有很强的观赏性.如图所示,abcdef为同一竖直平面内的滑行轨道,其中bc段水平,ab、dc和ef均为倾角θ=37°的斜直轨道,轨道间均用小圆弧平滑相连(小圆弧的长度可忽略).已知H1=5m,L=15m,H2=1.25m,H3=12.75m,设滑板与轨道之间的摩擦力为它们间压力的k倍(k=0.25),运动员连同滑板的总质量m=60kg.运动员从a点由静止开始下滑从c点水平飞出,在de上着陆后,经短暂的缓冲动作后只保留沿斜面方向的分速度下滑,接着在def轨道上来回滑行,除缓冲外运动员连同滑板可视为质点,忽略空气阻力,取g=l0m/s2,sin37°=06,cos37°=0.8.求:(1)运动员从c点水平飞出时的速度大小vc;
(2)运动员在de着陆时,沿斜面方向的分速度大小v0;
(3)设运动员第一次和第四次滑上ef道时上升的最大高度分别为hl和h4,则h1:h4等于多少?
分析 (1)设运动员从a点到c点的过程中克服阻力做功Wf,根据动能定理及摩擦力做功公式即可求解;
(2)运动员从c点水平飞出到落到de轨道上的过程中做平抛运动,设从c点到着陆点经过的时间为t,根据平抛运动的基本公式及几何关系即可求解;
(3)设运动员第一次沿ed斜面向上滑的最大高度为h1',根据功能关系求出h1',同理可得,运动员第二次沿ef斜面向上滑的最大高度,以此类推,运动员第四次沿ef斜面向上滑的最大高度,即可求解.
解答 解:(1)设运动员从a点到c点的过程中克服阻力做功Wf,
根据动能定理得:mgH1-Wf=$\frac{1}{2}{mv}_{c}^{2}$-0…①
而Wf=$kmgcosθ•\overline{ab}+kmg•\overline{bc}②$
$L=abcosθ+\overline{bc}$…③
由①②③式并代入数据,解得vc=5m/s…④
(2)运动员从c点水平飞出到落到de轨道上的过程中做平抛运动,设从c点到着陆点经过的时间为t
水平位移x=vxt…⑤
竖直位移 $y=\frac{1}{2}g{t}^{2}⑥$
由几何关$\frac{y-{H}_{2}}{x}=tanθ$…⑦
水平方向分速度vx=vc…⑧
竖直方向分速度vy=gt…⑨
v0=vxcosθ+vysinθ…⑩
由④⑤⑥⑦⑧⑨⑩式并代入数据,解得v0=10m/s
(3)设运动员第一次沿ed斜面向上滑的最大高度为h1',
根据功能关 $mg({h}_{1}-{h}_{2})=kmgcosθ(\frac{{h}_{1}}{sinθ}-\frac{{h}_{1}^{′}}{sinθ})$
解得 ${h}_{1}^{′}=\frac{1}{2}{h}_{1}$
同理可得,运动员第二次沿ef斜面向上滑的最大高度 ${h}_{2}=\frac{1}{2}{h}_{1}^{′}=(\frac{1}{2})^{2}{h}_{1}$
以此类推,运动员第四次沿ef斜面向上滑的最大高 ${h}_{4}=(\frac{1}{2})^{6}{h}_{1}$
解得 $\frac{{h}_{4}}{{h}_{1}}$=$\frac{1}{64}$
答:(1)运动员从c点水平飞出时的速度大小vc为5m/s;
(2)运动员在de上着陆时,沿斜面方向的分速度大小v0为10m/s;
(3)设运动员第一次和第四次滑上ef轨道时上升的最大高度分别为h1和h4,则h1:h4等于1:64
点评 本题主要考查了功能关系、动能定理及平抛运动基本公式的应用,知道平抛运动落在斜面上,竖直方向上的位移和水平方向上的位移的比值是定值,根据该关系可求出时间.难度较大.

 如图所示,在x轴上方有匀强磁场,从原点O射入1、2两个相同的负离子,射入时的速率也相同,且都与磁场方向垂直,只是1的速度方向与-x轴夹角为θ,2的速度方向与x轴夹角为θ.它们射出磁场点的坐标分别为x1和x2,在磁场中运行的时间分别为t1和t2,则( )
如图所示,在x轴上方有匀强磁场,从原点O射入1、2两个相同的负离子,射入时的速率也相同,且都与磁场方向垂直,只是1的速度方向与-x轴夹角为θ,2的速度方向与x轴夹角为θ.它们射出磁场点的坐标分别为x1和x2,在磁场中运行的时间分别为t1和t2,则( )| A. | x1=x2 | B. | x1<x2 | C. | $\frac{{t}_{1}}{{t}_{2}}$=1 | D. | $\frac{{t}_{1}}{{t}_{2}}$=$\frac{(π-θ)}{θ}$ |
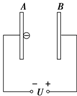 如图所示,在A板附近有一电子由静止开始向B板运动,则关于电子到达B板时的速率,下列解释正确的是( )
如图所示,在A板附近有一电子由静止开始向B板运动,则关于电子到达B板时的速率,下列解释正确的是( )| A. | 两板间距越大,加速的时间就越长,则获得的速率越大 | |
| B. | 两板间距越小,加速的时间就越长,则获得的速率越大 | |
| C. | 两板间距离越小,加速的时间越短,则获得的速率越小 | |
| D. | 获得的速率大小与两板间的距离无关,仅与加速电压U有关 |

| A. | 它的周期是1.0s | B. | 它的峰值是4A | C. | 它的有效值是2$\sqrt{2}$A | D. | 它的频率是0.8Hz |
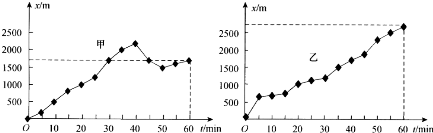
| A. | 在这一小时内,甲的平均速度较大 | |
| B. | 在这一小时内,乙的平均速度较大 | |
| C. | 在这一小时内,甲总是朝着一个方向运动 | |
| D. | 在这一小时内,乙总是朝着一个方向运动 |
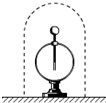 如图所示,一个验电器用金属网罩罩住,当加上水平向右的、场强大小为E的匀强电场时,验电器的箔片不张开填“张开”或“不张开”),我们把这种现象称之为静电屏蔽.此时,金属网罩的感应电荷在网罩内部空间会激发一个电场,它的场强与外部场强的关系是大小相等反向相反.
如图所示,一个验电器用金属网罩罩住,当加上水平向右的、场强大小为E的匀强电场时,验电器的箔片不张开填“张开”或“不张开”),我们把这种现象称之为静电屏蔽.此时,金属网罩的感应电荷在网罩内部空间会激发一个电场,它的场强与外部场强的关系是大小相等反向相反.