题目内容
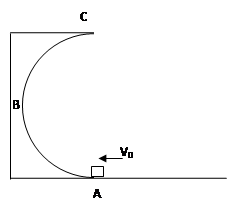
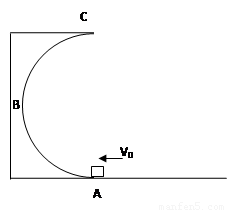
 质量为m的物体由半圆形轨道顶端从静止开始释放,如图所示,A为轨道最低点,A与圆心0在同一竖直线上,已知圆弧轨道半径为R,运动到A点时,轨道对物体的支持力大小为2.5mg,求此过程中物体克服摩擦力做的功.
质量为m的物体由半圆形轨道顶端从静止开始释放,如图所示,A为轨道最低点,A与圆心0在同一竖直线上,已知圆弧轨道半径为R,运动到A点时,轨道对物体的支持力大小为2.5mg,求此过程中物体克服摩擦力做的功.分析:根据牛顿第二定律,可求物体在A点的速度;根据动能定理可求解摩擦力做功.
解答:解:设物体在A点的速度为vA,由牛顿第二定律得:
2.5mg-mg=
则:vA=
设物体下滑过程克服阻力做功W,由动能定理得:
mgR-W=
m
-0
解得:W=0.25mgR
答:此过程中物体克服摩擦力做的功为0.25mgR
2.5mg-mg=
m
| ||
| R |
则:vA=
| 1.5gR |
设物体下滑过程克服阻力做功W,由动能定理得:
mgR-W=
| 1 |
| 2 |
| v | 2 A |
解得:W=0.25mgR
答:此过程中物体克服摩擦力做的功为0.25mgR
点评:本题考查了牛顿第二定律和动能定理的应用,难度不大.

练习册系列答案
相关题目
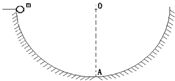
 质量为m的物体从半径为R光滑的半圆槽(质量为M)的A点由静止滑下,A、B等高,如图所示,关于物体m的运动,下列说法正确的是( )
质量为m的物体从半径为R光滑的半圆槽(质量为M)的A点由静止滑下,A、B等高,如图所示,关于物体m的运动,下列说法正确的是( ) 如图所示,质量为m的物体,从半径为R的光滑半圆槽的最上端由静止滑下,则下列说法中错误的是( )
如图所示,质量为m的物体,从半径为R的光滑半圆槽的最上端由静止滑下,则下列说法中错误的是( )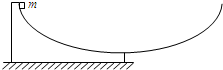 如图所示,质量为m的物体从半径为R的光滑半圆形槽顶部由静止开始滑下.则:①若半圆槽固定不动,物体可滑到右边最高处;②若半圆槽静止不动时,物体到达底部时动能等于mgR;③若半圆槽与桌面间无摩擦,物体可滑到右边最高处;④若半圆槽与桌面间无摩擦时,物体到达底部时动能等于mgR.以上说法中正确的有( )
如图所示,质量为m的物体从半径为R的光滑半圆形槽顶部由静止开始滑下.则:①若半圆槽固定不动,物体可滑到右边最高处;②若半圆槽静止不动时,物体到达底部时动能等于mgR;③若半圆槽与桌面间无摩擦,物体可滑到右边最高处;④若半圆槽与桌面间无摩擦时,物体到达底部时动能等于mgR.以上说法中正确的有( )