题目内容
【题目】如图所示，在某装置中有一匀强磁场，磁感应强度为B，方向垂直于xOy所在的纸面向外．某时刻在x＝l0，y＝0处，一质量为m、电荷量为＋2q的粒子a沿y轴负方向进入磁场；同一时刻，在x＝－l0，y＝0处，一质量为4m、电荷量为＋q的粒子b垂直磁场方向射入磁场．不计粒子的重力及其相互作用．
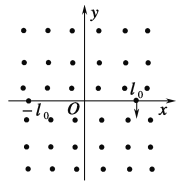
(1)如果粒子a经过坐标原点O，求它的速度为多大？
(2)如果粒子b与粒子a在坐标原点O相遇，粒子b的速度应为何值？方向如何？
【答案】(1) 
(2) 
方向与x轴的夹角为θ1＝
或θ2＝
【解析】(1)粒子a进入磁场的速度方向垂直于x轴，其运动轨迹的圆心在x轴上，又因粒子a经过坐标原点，故其轨道半径Ra＝
l0
设粒子a的速度为va，则有qBva＝m
解得va＝.
(2)粒子a做圆周运动的周期为Ta＝
粒子b做圆周运动的周期为Tb＝
＝2Ta
由于匀速圆周运动是周期性重复的运动，因而粒子a多次穿过坐标原点O，其时间为
ta＝Ta，
Ta，
Ta，…
粒子a与粒子b在O点相遇，根据粒子的周期关系，有
ta＝
Tb，
Tb，
Tb，…
因此，粒子b进入磁场处与O点之间的轨迹为圆周或圆周．两粒子的运动轨迹如图所示．
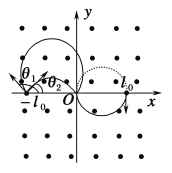
由几何关系得知粒子b的半径为Rb＝
l0
设粒子b的速度为vb，则有2qBvb＝4m
解得vb＝
粒子b运动的速度方向与x轴的夹角为θ1＝或θ2＝.
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
