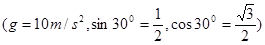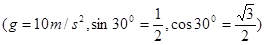题目内容
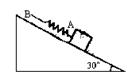
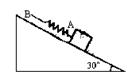
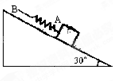 如图所示,弹簧AB原长为35cm,A端挂一个重50N的物体,手执B端,将物体置于倾角为30°的斜面上.当物体沿斜面匀速下滑时,弹簧长度为40cm;当物体匀速上滑时,弹簧长度为50cm,求:
如图所示,弹簧AB原长为35cm,A端挂一个重50N的物体,手执B端,将物体置于倾角为30°的斜面上.当物体沿斜面匀速下滑时,弹簧长度为40cm;当物体匀速上滑时,弹簧长度为50cm,求:(1)在图A和图B中分别画出物体下滑和上滑时的受力图
(2)弹簧的劲度系数
(3)物体与斜面的动摩擦因数(g=10m/s2,sin30°=
| 1 |
| 2 |
| ||
| 2 |
分析:物体做匀速运动,可对物体进行受力分析后应用平衡条件分别列式求解.
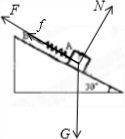
解答:解:(1)物体下滑,受重力、支持力、拉力和摩擦力(沿斜面向上),如图
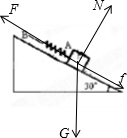
物体下滑时,受重力、支持力、拉力和摩擦力(沿斜面向下),如图
(2)匀速下滑时,设此时弹簧形变量为x1
则弹力F=kx1
由平衡条件得:
kx1+f=Gsin30°
N=Gcos30°
匀速上滑时,设此时弹簧形变量为:x2
则弹力F=kx2
由平衡条件得:
kx2=Gsin30°+f
N=Gcos30°
得:k=
=250 N/m
(3)再由:f=μN=μGcos30°=Gsin30°-kx1
得:μ=
=
=0.289
答:(1)如图所示;
(2)弹簧的倔强系数250N/m;
(3)物体与斜面的滑动摩擦系数为0.289.

物体下滑时,受重力、支持力、拉力和摩擦力(沿斜面向下),如图

(2)匀速下滑时,设此时弹簧形变量为x1
则弹力F=kx1
由平衡条件得:
kx1+f=Gsin30°
N=Gcos30°
匀速上滑时,设此时弹簧形变量为:x2
则弹力F=kx2
由平衡条件得:
kx2=Gsin30°+f
N=Gcos30°
得:k=
| 2Gsin30° |
| x1+x2 |
(3)再由:f=μN=μGcos30°=Gsin30°-kx1
得:μ=
| Gsin30°-kx1 |
| Gcos30° |
| 50×0.5-250×0.05 |
| 50×0.866 |
答:(1)如图所示;
(2)弹簧的倔强系数250N/m;
(3)物体与斜面的滑动摩擦系数为0.289.
点评:本题虽然涉及到胡克定律,但是主要是物体受力平衡条件的应用,受力分析后应用平衡条件列式求解即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,弹簧AB原长为35cm,A端挂一个重50N的物体,手执B端,将物体置于倾角为30°的斜面上.当物体沿斜面匀速下滑时,弹簧长度为40cm;当物体匀速上滑时,弹簧长度为50cm,试求:
如图所示,弹簧AB原长为35cm,A端挂一个重50N的物体,手执B端,将物体置于倾角为30°的斜面上.当物体沿斜面匀速下滑时,弹簧长度为40cm;当物体匀速上滑时,弹簧长度为50cm,试求: