题目内容
如图所示，以A、B和C、D为端点的两半圆形光滑轨道固定于竖直平面内，一滑板静止在光滑水平地面上，左端紧靠B点，上表面所在平面与两半圆分别相切于B、C。一物块被轻放在水平匀速运动的传送带上E点，运动到A时刚好与传送带速度相同，然后经A沿半圆轨道滑下，再经B滑上滑板。滑板运动到C时被牢固粘连。物块可视为质点，质量为m，滑板质量M=2m，两半圆半径均为R，板长l =6．5R，板右端到C的距离L=5R，E距A为S=5R，物块与传送带、物块与滑板间的动摩擦因素均为μ=0．5，重力加速度取g．
1.求物块滑到B点的速度大小；
2.分析物块从B点滑上滑板后，能否从滑板上滑落到水平地面；
3.分析滑块到达C点时的动能能否使滑块沿CD轨道滑到CD轨道的中点。
【答案】
1.vB=3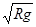
2.滑块未掉下滑板
3.滑块不能滑到CD轨道中点
【解析】（1）物块由E经过A到达B点的过程，由动能定理：
μmgs+mg·2R=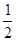
mvB2
解得： vB=3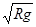
（2）m滑动的加速度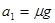
，M滑动的加速度
，
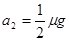假设t时刻二者达到共同速度，则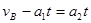
解得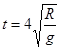
则此过程m的位移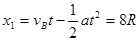
M的位移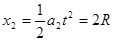
二者位移之差△x= x1—x2=6R＜6．5R，即滑块未掉下滑板
（3） m从B点滑到C点的过程中，克服摩擦力做功
Wf=μmgx1+μmg（l—△x）=4．25mgR
由动能定理：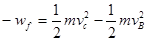
解得C点动能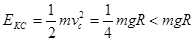
所以滑块不能滑到CD轨道中点。
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
如图所示，以A、B和C、D为端点的半径为R=0.6m的两半圆形光滑绝缘轨道固定于竖直平面内，B端、C端与光滑绝缘水平面平滑连接．A端、D端之间放一绝缘水平传送带，传送带下方B、C之间的区域存在水平向右的匀强电场，场强E=5×105V/m．当传送带以v0=6m/s 的速度沿图示方向匀速运动时，将质量为m=4×10-3kg，带电量q=+1×10-8C的小物块由静止放上传送带的最右端，小物块第一次运动到传送带最左端时恰好能从A点沿半圆轨道滑下，不计小物块大小及传送带与半圆轨道间的距离，g取10m/s2，已知A、D端之间的距离为1.2m 等于水平传送带的长．
（2011?广东）如图所示，以A、B和C、D为端点的两半圆形光滑轨道固定于竖直平面内，一滑板静止在光滑水平地面上，左端紧靠B点，上表面所在平面与两半圆分别相切于B、C，一物块被轻放在水平匀速运动的传送带上E点，运动到A时刚好与传送带速度相同，然后经A沿半圆轨道滑下，再经B滑上滑板，滑板运动到C时被牢固粘连，物块可视为质点，质量为m，滑板质量M=2m，两半圆半径均为R，板长l=6.5R，板右端到C的距离L在R＜L＜5R范围内取值，E距A为S=5R，物块与传送带、物块与滑板间的动摩擦因数均μ=0.5，重力加速度取g．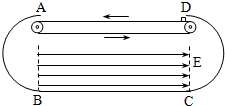
如图所示，以A、B和C、D为端点的半径为R=0.6m的两半圆形光滑绝缘轨道固定于竖直平面内，B端、C端与光滑绝缘水平地面平滑连接．A端、D端之间放一绝缘水平传送带．传送带下方B、C之间的区域存在水平向右的匀强电场，场强E=5×105V/m．当传送带以6m/s的速度沿图示方向匀速运动时，现将质量为m=4×10-3kg，带电量q=+1×10-8C的物块从传送带的右端由静止放上传送带．小物块运动第一次到A时刚好能沿半圆轨道滑下．不计小物块大小及传送带与半圆轨道间的距离，g取10m/s2，已知A、D端之间的距离为1.2m．求：
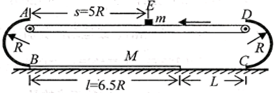如图所示，以A、B和C、D为断点的两半圆形光滑轨道固定于竖直平面内，一滑板静止在光滑的地面上，左端紧靠B点，上表面所在平面与两半圆分别相切于B、C两点，一物块（视为质点）被轻放在水平匀速运动的传送带上E点，运动到A点时刚好与传送带速度相同，然后经A点沿半圆轨道滑下，再经B点滑上滑板，滑板运动到C点时被牢固粘连．物块可视为质点，质量为m，滑板质量为M=2m，两半圆半径均为R，板长l=6.5R，板右端到C点的距离L在R＜L＜5R范围内取值，E点距A点的距离s=5R，物块与传送带、物块与滑板间的动摩擦因数均为μ=0.5，重力加速度g已知．