题目内容
图(a)所示的装置中，小物块A、B质量均为m，水平面上PQ段长为l，与物块间的动摩擦因数为μ，其余段光滑．初始时，挡板上的轻质弹簧处于原长；长为r的连杆位于图中虚线位置；A紧靠滑杆(A、B间距大于2r)．随后，连杆以角速度ω匀速转动，带动滑杆作水平运动，滑杆的速度－时间图像如图(b)所示．A在滑杆推动下运动，并在脱离滑杆后与静止的B发生完全非弹性碰撞．
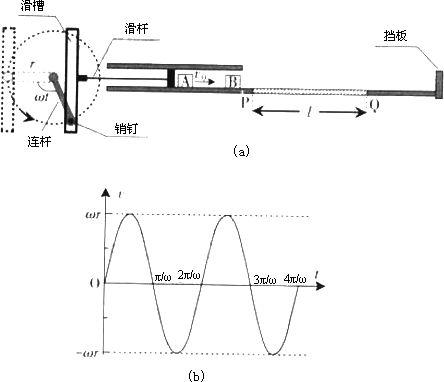
(1)求A脱离滑杆时的速度vo，及A与B碰撞过程的机械能损失ΔE．
(2)如果AB不能与弹簧相碰，设AB从P点到运动停止所用的时间为t1，求ω得取值范围，及t1与ω的关系式．
(3)如果AB能与弹簧相碰，但不能返回道P点左侧，设每次压缩弹簧过程中弹簧的最大弹性势能为Ep，求ω的取值范围，及Ep与ω的关系式(弹簧始终在弹性限度内)．
答案：
解析：
解析：
|
(1)设连杆的水平位移为x取水平向右的方向为正则： V0＝ AB相碰由动量守恒得：mv0＝2mv② AB系统机械能损失ΔE＝ 由①②③得： (2)AB在pq上做匀减速直线运动，加速度为： s≤1⑥ 0＝v＋at1⑦ 由④⑤⑥⑦得： (3)AB从p开始到弹簧压缩到最短时过程由能量守恒得： 可得到： 设AB返回时刚好到达P点时速度为0，则此时角速度最大 全过程由能量守恒得： 解得： |
求导得：
符合图像b当x＝0时，A与连杆分离，此时：
①
③
④
由运动学规律公式得AB开始到停止的位移：
⑤
⑧
综合⑧得到角速度的范围为：
练习册系列答案
相关题目
是电流表，实验发现，当用某种频率的单色光照射K时，K会发出电子（光电效应），这时，即使A、K之间的电压等于零，回路中也有电流．当A的电势低于K时，当A比K的电势低到某一值Uc时，电流消失，Uc称为截止电压，当改变照射光的频率ν，截止电压Uc也将随之改变，其关系如图2所示，如果某次实验我们测出了画出这条图线所需的一系列数据，又知道了电子电量，则 （ ）
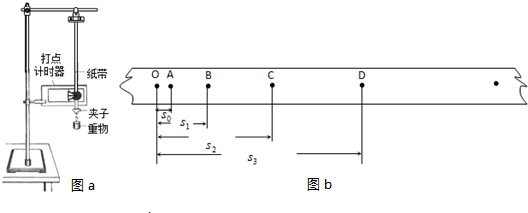
某同学设计了如图a所示的装置来探究加速度与力的关系．轻质弹簧秤固定在一合适的木块上，桌面的右边缘固定一个光滑的定滑轮，细绳的两端分别与弹簧秤的挂钩和矿泉水瓶连接．在桌面上做标记P、Q，并测出间距为d．开始时将木块置于P处，现缓慢向瓶中加水，直到木块刚刚开始运动为止，记下弹簧秤的示数F，然后释放木块，并用数字计时器记下木块从P运动到Q处的时间为t．