题目内容
4. 小明乘坐叔叔的车去郊区游玩,在车启动的同时,小明利用自己的电子表开始计时并观察汽车速度表的指针指示变化情况,在t1=8s的时间内,速度表上的指针从指向O位置匀速转到指向72位置(如图所示),此时汽车达到额定功率,此后,汽车保持额定功率不变,16s末指针转到指向108位置后,指针位置不再摆动,30s末关闭汽车发动机,36s末汽车静止,设汽车所受阻力恒定,汽车的质量为m=2×103kg,g取10m/s2,求:
小明乘坐叔叔的车去郊区游玩,在车启动的同时,小明利用自己的电子表开始计时并观察汽车速度表的指针指示变化情况,在t1=8s的时间内,速度表上的指针从指向O位置匀速转到指向72位置(如图所示),此时汽车达到额定功率,此后,汽车保持额定功率不变,16s末指针转到指向108位置后,指针位置不再摆动,30s末关闭汽车发动机,36s末汽车静止,设汽车所受阻力恒定,汽车的质量为m=2×103kg,g取10m/s2,求:(1)画出汽车运动的v-t图象;
(2)汽车所受到的阻力大小;
(3)前8s内汽车的牵引力;
(4)汽车在加速运动过程中位移的大小.
分析 (1)0-8s内汽车先做匀加速直线运动,8-16s内做变加速直线运动,16-30s内做匀速直线运动,30-36s内做匀减速直线运动,作出速度时间图线.
(2)根据匀减速运动的图线得出加速度大小,结合牛顿第二定律求出阻力的大小.
(3)根据速度时间图线求出匀加速运动的加速度,结合牛顿第二定律求出牵引力的大小.
(4)根据P=Fv求出汽车的额定功率,结合动能定理求出变加速运动的位移,根据匀加速运动的位移,求出汽车加速过程中的位移大小.
解答 解:(1)0-8s内汽车先做匀加速直线运动,8-16s内做变加速直线运动,16-30s内做匀速直线运动,30-36s内做匀减速直线运动.速度时间图线如图所示.
(2)匀减速运动的加速度大小${a}_{2}=\frac{30}{6}m/{s}^{2}=5m/{s}^{2}$,
根据牛顿第二定律得,汽车所受的阻力大小f=ma2=2000×5N=10000N.
(3)前8s内的加速度${a}_{1}=\frac{20}{8}m/{s}^{2}=2.5m/{s}^{2}$,
根据牛顿第二定律得,F-f=ma,解得F=f+ma=10000+2000×2.5N=15000N.
(4)0-8s内的位移${x}_{1}=\frac{1}{2}×8×20m=80m$,
额定功率P=Fv1=15000×20W=300000W,
根据动能定理得,$P{t}_{2}-f{x}_{2}=\frac{1}{2}m{{v}_{2}}^{2}-\frac{1}{2}m{{v}_{1}}^{2}$,
代入数据解得x2=190m.
则加速运动的位移x=x1+x2=80+190m=270m.
答:(1)汽车运动的速度时间图线如图所示.
(2)汽车所受的阻力大小为10000N.
(3)前8s内汽车的牵引力为15000N.
(4)汽车在加速运动过程中位移的大小为270m.
点评 解决本题的关键理清汽车在整个过程中的运动规律,结合牛顿第二定律和运动学公式综合求解,难度中等.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 课上老师做了这样一个实验:如图所示,用一象棋子压着一纸条,放在水平桌面上接近边缘处.第一次,慢拉纸条,将纸条抽出,棋子掉落在地上的P点;第二次,将棋子、纸条放回原来的位置,快拉纸条,将纸条抽出,棋子掉落在地上的N点.从第一次到第二次现象的变化,下列解释正确的是( )
课上老师做了这样一个实验:如图所示,用一象棋子压着一纸条,放在水平桌面上接近边缘处.第一次,慢拉纸条,将纸条抽出,棋子掉落在地上的P点;第二次,将棋子、纸条放回原来的位置,快拉纸条,将纸条抽出,棋子掉落在地上的N点.从第一次到第二次现象的变化,下列解释正确的是( )| A. | 棋子的惯性变大了 | B. | 棋子受到纸带的摩擦力变小了 | ||
| C. | 棋子受到纸带的冲量变小了 | D. | 棋子离开桌面时的动量变小了 |
 在如图所示的电路中,E为电源的电动势,r为电源的内电阻,R1、R2为可变电阻.在下列叙述的操作中,可以使灯泡L的亮度变亮的是( )
在如图所示的电路中,E为电源的电动势,r为电源的内电阻,R1、R2为可变电阻.在下列叙述的操作中,可以使灯泡L的亮度变亮的是( )| A. | 仅使R2的阻值增大 | B. | 仅使R2的阻值减小 | ||
| C. | 仅使R1的阻值增大 | D. | 仅使R1的阻值减小 |
 在一次运动会上,某同学抛出铅球的部分运动轨迹如图所示,已知在B点时铅球的速度与加速度相互垂直,空气阻力忽略不计,则下列说法中正确的是( )
在一次运动会上,某同学抛出铅球的部分运动轨迹如图所示,已知在B点时铅球的速度与加速度相互垂直,空气阻力忽略不计,则下列说法中正确的是( )| A. | D点的速率比C点的速率小 | |
| B. | A到B的过程中重力做正功 | |
| C. | 铅球运动过程中加速度不断变化 | |
| D. | B到E的过程中重力的瞬时功率不断增大 |
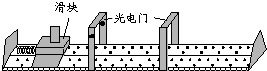 某同学用如图所示装置探究弹簧弹性势能与形变量的关系,弹簧的左端固定在气垫导轨上,遮光片的宽度为d,滑块和遮光板的质量为m.用滑块压缩弹簧,放手后滑块向右运动,用x表示弹簧的压缩量,t表示遮光片通过光电门的时间.
某同学用如图所示装置探究弹簧弹性势能与形变量的关系,弹簧的左端固定在气垫导轨上,遮光片的宽度为d,滑块和遮光板的质量为m.用滑块压缩弹簧,放手后滑块向右运动,用x表示弹簧的压缩量,t表示遮光片通过光电门的时间. 如图所示,线圈L与灯泡并联后接到电源上.先闭合开关S,稳定后设通过线圈L的电流为I1,通过小灯泡的电流为I2.现断开开关S,则通过小灯泡的电流方向反向(填“不变”或“反向”);若实验中发现小灯泡闪亮一下再熄灭,则说明I1>I2(填“>”、“<”或“=”).
如图所示,线圈L与灯泡并联后接到电源上.先闭合开关S,稳定后设通过线圈L的电流为I1,通过小灯泡的电流为I2.现断开开关S,则通过小灯泡的电流方向反向(填“不变”或“反向”);若实验中发现小灯泡闪亮一下再熄灭,则说明I1>I2(填“>”、“<”或“=”).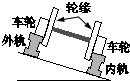 如图所示为火车车轮在转弯处的截面示意图,轨道的外轨高于内轨,在此转弯处规定火车的行驶速度为v.若火车通过此弯道时超速了,则火车的轮缘会挤压外轨;若火车通过此弯道时速度小于v,则火车的轮缘会挤压内轨.(填“内”或“外”)
如图所示为火车车轮在转弯处的截面示意图,轨道的外轨高于内轨,在此转弯处规定火车的行驶速度为v.若火车通过此弯道时超速了,则火车的轮缘会挤压外轨;若火车通过此弯道时速度小于v,则火车的轮缘会挤压内轨.(填“内”或“外”) 如图所示,质量m1=2.8kg的物体A放在水平地面上,与地面的动摩擦因数μ1=0.2,质量m2=2kg的物体B放在A的竖直前表面上,A、B间动摩擦因数μ2=0.5,如图所示,问至少用多大的力才可以使B相对于A保持静止状态.
如图所示,质量m1=2.8kg的物体A放在水平地面上,与地面的动摩擦因数μ1=0.2,质量m2=2kg的物体B放在A的竖直前表面上,A、B间动摩擦因数μ2=0.5,如图所示,问至少用多大的力才可以使B相对于A保持静止状态.