题目内容
5.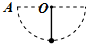 如图所示,长度为L的轻绳一端固定在0点,另一端系着质量为m的小球.把小球从与0点等高的A处由静止释放(此时轻绳伸直〕,运动过程中小球受到空气阻力的作用,经过最低点时绳子张力大小为2.5mg,则在此过程中小球克服空气阻力所做的功为( )
如图所示,长度为L的轻绳一端固定在0点,另一端系着质量为m的小球.把小球从与0点等高的A处由静止释放(此时轻绳伸直〕,运动过程中小球受到空气阻力的作用,经过最低点时绳子张力大小为2.5mg,则在此过程中小球克服空气阻力所做的功为( )| A. | mgL | B. | $\frac{mgL}{2}$ | C. | $\frac{mgL}{3}$ | D. | $\frac{mgL}{4}$ |
分析 首先求出小球到达最低点时的速度:小球经过最低点时,由绳子的拉力和重力的合力充当向心力,即可由牛顿第二定律求出在最低点的速度;
小球从A点到最低点的过程中,重力做功mgL,空气阻力做功,绳子的拉力不做功,空气阻力是变力,可根据动能定理求小球克服空气阻力做的功.
解答 解:小球在最低点,由牛顿第二定律得:
F-mg=m$\frac{{v}^{2}}{L}$
由题有:F=2.5mg,
则得:mv2=1.5mgL
从A点到最低点的过程中,根据动能定理得:
-Wf+mgL=$\frac{1}{2}m{v}^{2}$-0
则得小球克服空气阻力所做的功为:Wf=$\frac{mgL}{4}$
故选:D
点评 本题是动能定理与向心力的综合,要注意空气阻力是变力,不能直接用功的公式求其做功,运用动能定理求解变力做功经常采用的方法,要熟练掌握.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
15.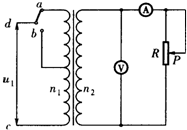 如图所示,理想变压器原、副线圈的匝数比为10:1,b是原线圈的中心抽头,电压表和电流表均为理想电表,从某时刻开始在原线圈c、d两端加上交变电压,其瞬时值表达式为u1=220$\sqrt{2}$sin100πtV,则( )
如图所示,理想变压器原、副线圈的匝数比为10:1,b是原线圈的中心抽头,电压表和电流表均为理想电表,从某时刻开始在原线圈c、d两端加上交变电压,其瞬时值表达式为u1=220$\sqrt{2}$sin100πtV,则( )
 如图所示,理想变压器原、副线圈的匝数比为10:1,b是原线圈的中心抽头,电压表和电流表均为理想电表,从某时刻开始在原线圈c、d两端加上交变电压,其瞬时值表达式为u1=220$\sqrt{2}$sin100πtV,则( )
如图所示,理想变压器原、副线圈的匝数比为10:1,b是原线圈的中心抽头,电压表和电流表均为理想电表,从某时刻开始在原线圈c、d两端加上交变电压,其瞬时值表达式为u1=220$\sqrt{2}$sin100πtV,则( )| A. | 交流电的频率为50Hz | |
| B. | 当单刀双掷开关与a连接时,电压表的示数为22V | |
| C. | 当t=$\frac{1}{600}$s时,c、d间的电压瞬时值为110V | |
| D. | 单刀双掷开关与a连接,在滑阻触头P向上移动过程中,电压表和电流表的示数均变小 | |
| E. | 单刀双掷开关由a扳向b,电压表和电流表的示数均变小 | |
| F. | 单刀双掷开关由a扳向b,变压器输出功率变大 |
16.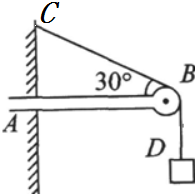 如图所示,水平横梁一端插在墙壁内,另一端装有光滑的小滑轮B.一轻绳的一端 C固定于墙壁上,另一端跨过滑轮后悬挂一质量m=8kg的重物,∠CBA=30°,g取10N/kg,则下列说法正确的是( )
如图所示,水平横梁一端插在墙壁内,另一端装有光滑的小滑轮B.一轻绳的一端 C固定于墙壁上,另一端跨过滑轮后悬挂一质量m=8kg的重物,∠CBA=30°,g取10N/kg,则下列说法正确的是( )
 如图所示,水平横梁一端插在墙壁内,另一端装有光滑的小滑轮B.一轻绳的一端 C固定于墙壁上,另一端跨过滑轮后悬挂一质量m=8kg的重物,∠CBA=30°,g取10N/kg,则下列说法正确的是( )
如图所示,水平横梁一端插在墙壁内,另一端装有光滑的小滑轮B.一轻绳的一端 C固定于墙壁上,另一端跨过滑轮后悬挂一质量m=8kg的重物,∠CBA=30°,g取10N/kg,则下列说法正确的是( )| A. | 滑轮对绳子的作用力方向水平向右 | |
| B. | 滑轮受到绳子的作用力大小为80 N | |
| C. | BC段绳子的拉力为80N | |
| D. | BC段绳子的拉力大于BD段绳子的拉力 |
13. 某飞机着陆时的速度是60m/s,随后减速滑行,如果飞机的平均加速度大小是2m/s2.为了使飞机能够安全地停下来,则滑道的长度至少为( )
某飞机着陆时的速度是60m/s,随后减速滑行,如果飞机的平均加速度大小是2m/s2.为了使飞机能够安全地停下来,则滑道的长度至少为( )
 某飞机着陆时的速度是60m/s,随后减速滑行,如果飞机的平均加速度大小是2m/s2.为了使飞机能够安全地停下来,则滑道的长度至少为( )
某飞机着陆时的速度是60m/s,随后减速滑行,如果飞机的平均加速度大小是2m/s2.为了使飞机能够安全地停下来,则滑道的长度至少为( )| A. | 900m | B. | 90m | C. | 1800m | D. | 180m |
20.如果一个系统不受外力,或者所受外力的矢量和为零,这个系统的总动量保持不变.这就是动量守恒定律.若一个系统动量守恒时,则( )
| A. | 此系统内每个物体所受的合力一定都为零 | |
| B. | 此系统内每个物体的动量大小不可能都增加 | |
| C. | 此系统的机械能一定守恒 | |
| D. | 此系统的机械能可能增加 |
10.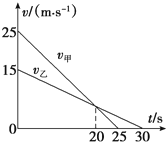 秋冬交替季节,贵州山区雾天增多,能见度大大降低.在这样的恶劣天气中,甲、乙两汽车在一条平直的单行道上,乙在前、甲在后同向行驶.某时刻两车司机同时听到前方有事故发生的警笛提示,同时开始刹车,结果两辆车发生了碰撞.图示为两辆车刹车后若不相撞的v-t图象,由此可知( )
秋冬交替季节,贵州山区雾天增多,能见度大大降低.在这样的恶劣天气中,甲、乙两汽车在一条平直的单行道上,乙在前、甲在后同向行驶.某时刻两车司机同时听到前方有事故发生的警笛提示,同时开始刹车,结果两辆车发生了碰撞.图示为两辆车刹车后若不相撞的v-t图象,由此可知( )
 秋冬交替季节,贵州山区雾天增多,能见度大大降低.在这样的恶劣天气中,甲、乙两汽车在一条平直的单行道上,乙在前、甲在后同向行驶.某时刻两车司机同时听到前方有事故发生的警笛提示,同时开始刹车,结果两辆车发生了碰撞.图示为两辆车刹车后若不相撞的v-t图象,由此可知( )
秋冬交替季节,贵州山区雾天增多,能见度大大降低.在这样的恶劣天气中,甲、乙两汽车在一条平直的单行道上,乙在前、甲在后同向行驶.某时刻两车司机同时听到前方有事故发生的警笛提示,同时开始刹车,结果两辆车发生了碰撞.图示为两辆车刹车后若不相撞的v-t图象,由此可知( )| A. | 两辆车刹车时的距离可能等于112.5m | |
| B. | 两辆车刹车时的距离可能等于90m | |
| C. | 两辆车一定是在刹车后的20s之内的某时刻发生相撞的 | |
| D. | 两辆车一定是在刹车20s以后的某时刻发生相撞的. |
17.下列各组物理量中,全部都是矢量的是( )
| A. | 位移、加速度、速度、时间 | B. | 速度、路程、时间、平均速度 | ||
| C. | 位移、速度、加速度、平均速度 | D. | 速度、质量、加速度、路程 |
14.一带负电粒子在电场中仅受电场力作用做匀速圆周运动,该电场可能是( )
| A. | 匀强电场 | B. | 负点电荷的电场 | ||
| C. | 两个等量异种负点电荷的电场 | D. | 两个等量同种正点电荷的电场 |
15.下列关于速度和加速度的说法中,正确的是( )
| A. | 加速度是描述物体速度变化快慢的物理量 | |
| B. | 物体的速度为零,加速度不一定为零 | |
| C. | 运动物体的加速度越来越小,表示速度变化的越来越慢 | |
| D. | 运动物体的加速度越来越小,表示物体运动的速度也越来越小 |