题目内容
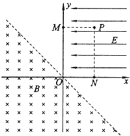
【题目】如图所示，空间内有相距为d的两块正对的平行金属板PQ、MN，两板带等量异种电荷，板间匀强电场的场强为
．在虚线QN右侧存在垂直于纸面、磁感应强度大小未知的矩形匀强磁场(图中未画出)．现有一质量为m、电量为q的带电粒子以初速度v0沿两板中央OO′射入，并恰好从下极板边缘射出，又经过在矩形有界磁场中的偏转，最终从金属板PQ的右端进入平行金属板PQ、MN之间．不计带电粒子重力．求：
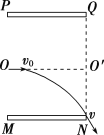
（1）粒子从下极板边缘射出时速度大小和方向；
（2）虚线QN右侧匀强磁场的磁感应强度大小；
（3）矩形有界磁场的最小面积．
【答案】（1）2v0，速度方向与QN方向之间的夹角为30°；（2）
；（3）(2＋
)d2.
【解析】
（1）带电粒子做平抛运动，由运动的分解可得平行极板方向做匀速运动，垂直此方向做匀加速运动，根据运动学公式即可求解；
（2）粒子做平抛运动后进入磁场做匀速圆周运动，根据几何关系可得半径。再由
求出磁感应强度B；
（3）从几何角度得出磁场的最小区域，再由面积公式即可求解。
（1）在电场中，
解得vy＝v0
则粒子从下极板边缘射出时的速度为v＝
解得，v＝2v0
设速度方向与QN方向之间的夹角为θ，则有
解得，θ＝30°.
（2）带电粒子离开电场后进入匀强磁场，在匀强磁场中做匀速圆周运动，其轨迹如图所示
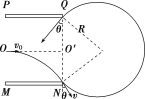
由几何关系可知，
解得
（3）由轨迹图可知，磁场区域宽度最小为R(1＋cos 30°)，长度最小等于2R；
所以矩形有界磁场的最小面积为S＝2R2(1＋cos 30°)＝(2＋)d2.
练习册系列答案
相关题目
