题目内容
11.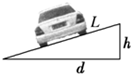 如图所示,在某外高内低的弯道测试路段上汽车向左转弯,把汽车的运动看作是在水平面内做半径为R的匀速圆周运动.设路面内外高度相差h,路基的水平宽度为d,路面的宽度为L,已知重力加速度为g.要使车轮与路面之间垂直前进方向的横向摩擦力等于零,则汽车转弯时的车速应等于( )
如图所示,在某外高内低的弯道测试路段上汽车向左转弯,把汽车的运动看作是在水平面内做半径为R的匀速圆周运动.设路面内外高度相差h,路基的水平宽度为d,路面的宽度为L,已知重力加速度为g.要使车轮与路面之间垂直前进方向的横向摩擦力等于零,则汽车转弯时的车速应等于( )| A. | $\sqrt{\frac{gRh}{L}}$ | B. | $\sqrt{\frac{gRL}{h}}$ | C. | $\sqrt{\frac{gRh}{d}}$ | D. | $\sqrt{\frac{gRd}{h}}$ |
分析 要使车轮与路面之间的横向摩擦力等于零,则汽车转弯时,由路面的支持力与重力的合力提供汽车的向心力,根据牛顿第二定律,结合数学知识求解车速
解答 解:设路面的斜角为θ.要使车轮与路面之间的横向摩擦力等于零,则汽车转弯时,由路面的支持力与重力的合力提供汽车的向心力,作出汽车的受力图,如图.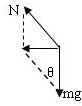
根据牛顿第二定律,得:
mgtanθ=m$\frac{{v}^{2}}{R}$
又由数学知识得到:
tanθ=$\frac{h}{d}$
联立解得:$v=\sqrt{\frac{gRh}{d}}$
故选:C
点评 本题是生活中圆周运动的问题,关键是分析物体的受力情况,确定向心力的来源.

练习册系列答案
相关题目
2. 如图所示,两带电平行金属板之间有相互正交的匀强电场和匀强磁场.现使一个带正电的粒子以某一初速沿垂直于电场和磁场的方向射入两极板间,测得它飞出该场区时的动能比射入时的动能小.为使带电粒子飞出场区时的动能比射入时的动能大,以下措施中可行的是( )
如图所示,两带电平行金属板之间有相互正交的匀强电场和匀强磁场.现使一个带正电的粒子以某一初速沿垂直于电场和磁场的方向射入两极板间,测得它飞出该场区时的动能比射入时的动能小.为使带电粒子飞出场区时的动能比射入时的动能大,以下措施中可行的是( )
 如图所示,两带电平行金属板之间有相互正交的匀强电场和匀强磁场.现使一个带正电的粒子以某一初速沿垂直于电场和磁场的方向射入两极板间,测得它飞出该场区时的动能比射入时的动能小.为使带电粒子飞出场区时的动能比射入时的动能大,以下措施中可行的是( )
如图所示,两带电平行金属板之间有相互正交的匀强电场和匀强磁场.现使一个带正电的粒子以某一初速沿垂直于电场和磁场的方向射入两极板间,测得它飞出该场区时的动能比射入时的动能小.为使带电粒子飞出场区时的动能比射入时的动能大,以下措施中可行的是( )| A. | 增大粒子射入时的速度 | |
| B. | 保持金属极板所带电荷量不变,增大两板间的距离 | |
| C. | 保持两极板间的距离不变,增大两金属极板所带的电荷量 | |
| D. | 减小磁场的磁感应强度 |
19.下列说法正确的是( )
| A. | 物体中分子热运动动能的总和等于物体的内能 | |
| B. | 橡胶无固定熔点,是非晶体 | |
| C. | 饱和汽压与分子密度有关,与温度无关 | |
| D. | 热机的效率总小于1 | |
| E. | 对于同一种气体,温度越高,分子平均动能越大 |
16.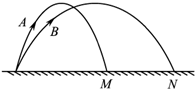 如图所示,从地面上同一位置抛出两小球A、B,分别落在地面上的M、N点,A球运动的最大高度大于B球运动的最大高度. 空气阻力不计,则( )
如图所示,从地面上同一位置抛出两小球A、B,分别落在地面上的M、N点,A球运动的最大高度大于B球运动的最大高度. 空气阻力不计,则( )
 如图所示,从地面上同一位置抛出两小球A、B,分别落在地面上的M、N点,A球运动的最大高度大于B球运动的最大高度. 空气阻力不计,则( )
如图所示,从地面上同一位置抛出两小球A、B,分别落在地面上的M、N点,A球运动的最大高度大于B球运动的最大高度. 空气阻力不计,则( )| A. | B的加速度比A的大 | B. | B飞行时间比A的飞行时间长 | ||
| C. | B在最高点的速度比A在最高点的大 | D. | A落地时的速度比B落地时的速度大 |
3.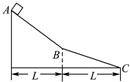 如图所示,一小物块在粗糙程度相同的两个固定斜面上从A经B滑动到C,如不考虑在B点机械能的损失,则( )
如图所示,一小物块在粗糙程度相同的两个固定斜面上从A经B滑动到C,如不考虑在B点机械能的损失,则( )
 如图所示,一小物块在粗糙程度相同的两个固定斜面上从A经B滑动到C,如不考虑在B点机械能的损失,则( )
如图所示,一小物块在粗糙程度相同的两个固定斜面上从A经B滑动到C,如不考虑在B点机械能的损失,则( )| A. | 从A到B和从B到C,减少的机械能相等 | |
| B. | 从A到B和从B到C,增加的动能相等 | |
| C. | 从A到B和从B到C,摩擦产生的热量相等 | |
| D. | 小物块在B点的动能一定最大 |
20.图1为一列简谐横波在t=0时的波形图,P是平衡位置在x=1cm处的质元,Q是平衡位置在x=4cm处的质元.图2为质元Q的振动图象,则( )
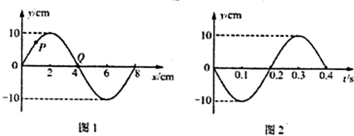

| A. | t=0.3s时,质元Q的加速度达到正向最大 | |
| B. | 波的传播速度为20m/s | |
| C. | t=0.7s时,质元P的运动方向沿y轴负方向 | |
| D. | 波的传播方向沿x轴负方向 |
1.下列说法中正确的是( )
| A. | 在光导纤维束内传送图象是利用光的衍射现象 | |
| B. | 用透明的标准样板和单色光检查平面的平整度是利用了光的干涉现象 | |
| C. | 全息照片往往用激光来拍摄,主要是利用了激光的相干性 | |
| D. | 拍摄玻璃橱窗内的物品时,往往在镜头前加一个偏振片以增加透射光的强度 | |
| E. | 海市蜃楼产生的原因是由于海面上上层空气的折射率比下层空气折射率小 |
 一块长为L=1m的粗糙均匀薄木板可绕其左端水平轴O在竖直面内由电动机带动转动,初始时处于水平位置,如图所示.一个小滑块以初速度v0=2m/s,加速度大小为a=$\sqrt{3}$m/s2,从左端向右滑动,滑到离左端$\frac{\sqrt{3}}{2}$L处时碰撞固定在板面上的触发开关P,速度立即减为零,同时板立即以一定的角度速度绕左端沿顺时针方向匀速转动,已知重力加速度g=10m/s2.求:
一块长为L=1m的粗糙均匀薄木板可绕其左端水平轴O在竖直面内由电动机带动转动,初始时处于水平位置,如图所示.一个小滑块以初速度v0=2m/s,加速度大小为a=$\sqrt{3}$m/s2,从左端向右滑动,滑到离左端$\frac{\sqrt{3}}{2}$L处时碰撞固定在板面上的触发开关P,速度立即减为零,同时板立即以一定的角度速度绕左端沿顺时针方向匀速转动,已知重力加速度g=10m/s2.求: