题目内容
【题目】如图所示，用长为l的绝缘细线拴一个质量为m、带电量为+q的小球（可视为质点）后悬挂于O点，整个装置处于水平向右的匀强电场中．将小球拉至使悬线呈水平的位置A后，由静止开始将小球释放，小球从A点开始向下摆动，当悬线转过
角到达位置B时，速度恰好为零．求：
（1）B、A两点的电势差UBA；
（2）电场强度E；
（3）小球到达B点时，悬线对小球的拉力T；
（4）小球从A运动到B点过程中的最大速度vm和悬线对小球的最大拉力Tm．
【答案】（1）
（2）
（3）
（4）
【解析】（1）小球由A到B过程中，由动能定理得：mgLsin60°-qUBA=0
所以
（2）场强
（3）小球在AB间摆动，由对称性得知，B处绳拉力与A处绳拉力相等，而在A处，由水平方向平衡有：FTA=Eq=
mg，所以FTB=FTA=
mg
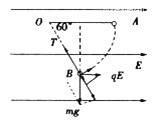
（4）将电场力和重力等效为F′，当速度与F′垂直时，速度最大，F′与水平方向的夹角为θ，
根据几何关系
得θ=30°，
根据动能定理，有：mgLsin30°Eq(LLcos30°)＝
m
解得
悬线对小球的拉力Tm、重力沿半径方向的分力mgsin300、电场力沿半径方向的分力qE cos300的合力是向心力：Tm – mgsin300– qEcos300= m
，
解得Tm =(6– 2
) mg．
练习册系列答案
相关题目
