题目内容
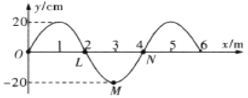
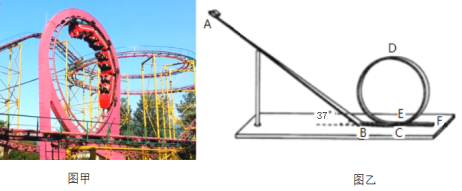
【题目】为了研究过山车的原理，某同学利用国庆假期体验了温州乐园的过山车（如图甲）。过山车轨道可以理想化为如图乙所示：一个与水平方向夹角为
、长为 L=12.0m 的倾斜轨道AB,通过水平轨道BC、半径R=2m的竖直圆形轨道与水平轨道EF相连,C为竖直轨道的最低点,D为最高点,E为出口,整个轨道摩擦力不计。其中轨道间都通过一小段长度可忽略的光滑圆弧相连。现使一质量m=1kg的物块（可看作质点）从倾斜轨道A点静止释放沿圆轨道运动。（g取10m/s2）求：
（1）物块滑到C点的速度大小
（2）物块通过D点时对轨道的压力
（3）设物块静止释放点离底部B点在斜面上的距离为x，为了使物块不脱离圆轨道运动，求x应该满足的条件。
【答案】（1）12m/s（2）22N，方向竖直向上（3）
或
【解析】
解：(1)从
到
，根据动能定理可得：
解得：
(2) (1)从到
，根据动能定理可得：
解得：
在点则有：
解得：
根据牛顿第三定律可得物块通过点时对轨道的压力
，方向竖直向上
(3) 滑块不脱离轨道有两种情况，第一是滑块进入圆形轨道后上升的最大高度不超过圆形轨道的半径，由功能原理可得：
解得：
第二种是滑块能通过轨道的轨道的最高点，
若滑块恰能通过圆形轨道的最高点，则有：
解得：
即滑块不脱离轨道的条件是：
或
练习册系列答案
名校课堂系列答案
相关题目
