题目内容
5. 静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线,图中φ0和d为已知量,一个带负电的粒子在电场中以x=0为中心,沿x轴方向做周期性运动,已知该粒子质量为m,电荷量为-q,其动能与电势能之和为-A(0<A<qφ0),忽略重力,求:
静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线,图中φ0和d为已知量,一个带负电的粒子在电场中以x=0为中心,沿x轴方向做周期性运动,已知该粒子质量为m,电荷量为-q,其动能与电势能之和为-A(0<A<qφ0),忽略重力,求:(1)粒子所受静电力的大小;
(2)粒子的运动区间;
(3)粒子的运动周期.
分析 (1)由图可知,电势随x均匀变化,则可知电场为匀强电场,由电势差与电场强度的关系可求得电场强度,即可求得电场力;
(2)由题意可知,动能与电势能之和保持不变,设出运动区间为[-x,x],由题意可知x处的电势,则由数学关系可求得x值;
(3)粒子在区间内做周期性变化,且从最远点到O点时做匀变速直线运动,则由运动学规律可求得周期.
解答 解:(1)由图可知,0与d(或-d)两点间的电势差为:U=φ0
电场强度的大小为:E=$\frac{φ{\;}_{0}}{d}$
电场力的大小为:F=qE=$\frac{qφ{\;}_{0}}{d}$.
(2)设粒子在[-x,x]区间内运动,速率为v,由题意得:
$\frac{1}{2}$mv2-qφ=-A
由图可知:φ=φ0(1-$\frac{|x|}{d}$)
由上解得:$\frac{1}{2}$mv2=qφ0(1-$\frac{|x|}{d}$)-A
因动能非负,有:qφ0(1-$\frac{|x|}{d}$)-A≥0
得:|x|≤d(1-$\frac{A}{q{φ}_{0}}$)
即:x=d(1-$\frac{A}{q{φ}_{0}}$)
粒子运动区间为:-d(1-$\frac{A}{q{φ}_{0}}$)≤x≤d(1-$\frac{A}{q{φ}_{0}}$).
(3)考虑粒子从-x0处开始运动的四分之一周期,根据牛顿第二定律,粒子的加速度为:
a=$\frac{F}{m}$=$\frac{qE}{m}$=$\frac{q{φ}_{0}}{md}$
由匀加速直线运动规律得:t=$\sqrt{\frac{2x}{a}}$
代入解得:t=$\sqrt{\frac{2m{d}^{2}}{q{φ}_{0}}(1-\frac{A}{q{φ}_{0}})}$
粒子运动周期为:T=4t=4$\sqrt{\frac{2m{d}^{2}}{q{φ}_{0}}(1-\frac{A}{q{φ}_{0}})}$
答:(1)粒子所受静电力的大小是$\frac{qφ{\;}_{0}}{d}$;
(2)粒子的运动区间是-d(1-$\frac{A}{q{φ}_{0}}$)≤x≤d(1-$\frac{A}{q{φ}_{0}}$);
(3)粒子的运动周期是4$\sqrt{\frac{2m{d}^{2}}{q{φ}_{0}}(1-\frac{A}{q{φ}_{0}})}$.
点评 本题难度较大,要求学生能从题干中找出可用的信息,同时能从图象中判断出电场的性质;并能灵活应用功能关系结合数学知识求解,故对学生的要求较高.

| A. | 电风扇 | B. | 电热毯 | C. | 日光灯 | D. | 家用电热水壶 |
| A. | 电磁波不能在真空中传播 | |
| B. | 变化的电场一定能产生变化的磁场 | |
| C. | 电磁波在真空中传播的速度是3×108m/s | |
| D. | 变化的电场和磁场由近及远地向周围空间传播形成电磁波 |
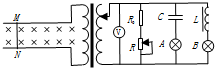 如图所示,理想变压器原线圈上连接着在水平面内的长直平行金属导轨,导轨之间存在垂直于导轨平面的匀强磁场,金属杆MN垂直放置在导轨上,且接触良好.移动变压器副线圈上的滑动触头可改变副线圈匝数,副线圈上接有一只理想电压表,滑动变阻器R的总阻值大于定值电阻R0的阻值,线圈L的直流电阻、导轨和金属杆的电阻都忽略不计.现在让金属杆以速度v=v0sin$\frac{2π}{T}$t的规律在导轨上左右来回运动,两灯A、B都发光.下列说法中正确的是( )
如图所示,理想变压器原线圈上连接着在水平面内的长直平行金属导轨,导轨之间存在垂直于导轨平面的匀强磁场,金属杆MN垂直放置在导轨上,且接触良好.移动变压器副线圈上的滑动触头可改变副线圈匝数,副线圈上接有一只理想电压表,滑动变阻器R的总阻值大于定值电阻R0的阻值,线圈L的直流电阻、导轨和金属杆的电阻都忽略不计.现在让金属杆以速度v=v0sin$\frac{2π}{T}$t的规律在导轨上左右来回运动,两灯A、B都发光.下列说法中正确的是( )| A. | 只增大T,则灯A变亮、灯B变暗 | |
| B. | 当时间t=T时,两灯都亮着,电压表的示数为零 | |
| C. | 只将变阻器R的滑片下滑时,通过副线圈的电流减小,电压表的示数变大 | |
| D. | 只增大v0,两灯都变亮,杆MN来回运动的最大距离变大 |
| A. | 时间、路程 | B. | 位移、路程 | C. | 速度、重力势能 | D. | 功、位移 |
| A. | 毫克 | B. | 克 | C. | 千克 | D. | 吨 |
| A. | 两种运动中,物体受到的合外力为零 | |
| B. | 两种运动中,动能不会变化 | |
| C. | 两种运动中的“匀速”的意思相同 | |
| D. | 匀速圆周运动是加速度不变的曲线运动 |
 某同学用多用电表测电阻,进行机械调零后,将选择开关旋到“×100”挡,让红、黑表笔直接相连(选填“直接相连”或“靠近但不接触”),调整“欧姆调零旋钮”,使指针指到“0Ω”;然后让红、黑表笔分别接触待测电阻的两端,多用电表的指针位置如图所示,则所测电阻的阻值为2600(选填“2600”或“26”)Ω.
某同学用多用电表测电阻,进行机械调零后,将选择开关旋到“×100”挡,让红、黑表笔直接相连(选填“直接相连”或“靠近但不接触”),调整“欧姆调零旋钮”,使指针指到“0Ω”;然后让红、黑表笔分别接触待测电阻的两端,多用电表的指针位置如图所示,则所测电阻的阻值为2600(选填“2600”或“26”)Ω. 如图所示,在竖直平面内倾斜放置的U形管,管的一端封闭,内有一段空气柱,U形管内的倾角为θ,U型管内水银柱长度L1、L2,如图所示,已知水银密度为ρ,大气压强为p0,则封闭段空气柱的压强为P0+L1sinθ.
如图所示,在竖直平面内倾斜放置的U形管,管的一端封闭,内有一段空气柱,U形管内的倾角为θ,U型管内水银柱长度L1、L2,如图所示,已知水银密度为ρ,大气压强为p0,则封闭段空气柱的压强为P0+L1sinθ.