题目内容
如图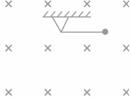
图
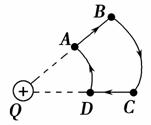
解析:欲求摆球通过最低位置时绳上的拉力F,需建立最低位置时小球的牛顿第二定律方程,再由能量观点求出最低位置时的速度即可.不过由于洛伦兹力方向与速度方向相关,本题应讨论向左、向右过最低位置的两种情况,不注意分析,往往容易漏解.
解:以摆球为研究对象.摆球在运动过程中受重力mg、弹力T及洛伦兹力F三力作用,其中弹力T、洛伦兹力F都随小球速度的改变而改变,但这两种力始终与摆球运动方向垂直,不做功,只有重力做功.
根据机械能守恒:mgL=![]() mvm2
mvm2
摆球向左经最低位置时由牛顿第二定律:T-mg-F=![]() 且F=Bqvm
且F=Bqvm
联立以上各式得:T=3mg+Bq![]()
当向右摆动,到最低点的速度向右时,F的方向则向上.
由牛顿第二定律:T+F-mg=![]()
联立解得:T=3mg-Bq![]() .
.

练习册系列答案
相关题目