一辆实验小车可沿水平地面上的长直轨道匀速向右运动．有一台发出细光束的激光器在小转台M上.到轨道的距离MN为d=10m.如图所示．转台匀速转动.使激光束在水平面内扫描.扫描一周的时间为T=60s．光束转动方向如图中箭头所示．当光束与MN的夹角为45°时.光束正好射到小车上．如果再经过△t=2.5s光束又射到小车上.则小车的速度是多少? 题目和参考答案——青夏教育精英家教网—

题目内容

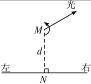
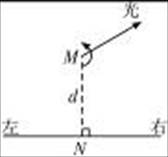
一辆实验小车可沿水平地面（图中纸面）上的长直轨道匀速向右运动．有一台发出细光束的激光器在小转台M上，到轨道的距离MN为d=10m，如图所示．转台匀速转动，使激光束在水平面内扫描，扫描一周的时间为T=60s．光束转动方向如图中箭头所示．当光束与MN的夹角为45°时，光束正好射到小车上．如果再经过△t=2.5s光束又射到小车上，则小车的速度是多少？（结果保留二位数字）

分析：当光束与MN的夹角为45°时，光束正好射到小车上，此时小车到N点的距离等于MN为d=10m，根据题意再经过△t=2.5（s），光束又射到小车上，因此要求小车的速度应先求出△t时间内光束转过的角度，再求出，△t时间内小车运动的距离，最后利用速度公式V=

计算出小车的速度．

解答：解：①作图

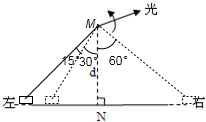
在△t内，光束转过角度△φ=

△t

×360°=15°②
由图可知L₁=d（tan45°-tan30°） ③
由②、③两式并代入数值，得
v₁=1.7m/s④
（2）光束照到小车时，小车正在远离N点，△t内光束与MN的夹角从45°变为60°，小车走过L₂，速度为
v₂=

△t

⑤
由图可知

L2=d（tan60°-tan45°） ⑥
由⑤、⑥两式并代入数值，得
v₂=2.9m/s
答：若小车正在接近N点，则小车的速度约为1.7m/s；若小车正在远离N点，则小车的速度约为2.9m/s．

点评：本题考查速度的计算，要熟记速度的计算公式，想方设法的找出相关的各个物理量，最后代入数值计算．

练习册系列答案

相关题目

一辆实验小车可沿水平地面(图中纸面)上的长直轨道匀速向右运动.有一台发出细光束的激光器装在小转台M上，到轨道的距离MN为d=10 m，如图14-10所示，转台匀速转动，使激光束在水平面内扫描，扫描一周的时间为T=60 s，光束转动方向如图中箭头所示，当光束与MN的夹角为45°时，光束正好射到小车上，如果再经过Δt=2.5 s光束又射到小车上，则小车的速度为多少？(结果保留两位有效数字)

图14-10

一辆实验小车可沿水平地面(图中标有左右的直线)上的长直轨道匀速向右运动.有一台发出细光束的激光器装在小转台M上，到轨道的距离为d="10" m，如图所示，转台匀速转动，使激光束在水平面内扫描，扫描一周的时间为T="60" s，光束转动方向如图中箭头所示，当光束与MN的夹角为45°时，光束正好射到小车上，如果再经过Δt="2.5" s光束又射到小车上，则小车的速度为多少？

一辆实验小车可沿水平地面(图中标有左右的直线)上的长直轨道匀速向右运动.有一台发出细光束的激光器装在小转台M上，到轨道的距离为d=10 m，如图所示，转台匀速转动，使激光束在水平面内扫描，扫描一周的时间为T=60 s，光束转动方向如图中箭头所示，当光束与MN的夹角为45°时，光束正好射到小车上，如果再经过Δt=2.5 s光束又射到小车上，则小车的速度为多少？

试题分类