题目内容
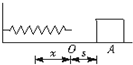 如图所示,轻弹簧一端固定在挡板上.质量为m的物体以初速度v0沿水平面开始运动,起点A与轻弹簧自由端O距离为s,物体与水平面间的动摩擦因数为μ,物体与弹簧相碰后,弹簧的最大压缩量为x,则弹簧被压缩最短时,弹簧具有的弹性势能为( )
如图所示,轻弹簧一端固定在挡板上.质量为m的物体以初速度v0沿水平面开始运动,起点A与轻弹簧自由端O距离为s,物体与水平面间的动摩擦因数为μ,物体与弹簧相碰后,弹簧的最大压缩量为x,则弹簧被压缩最短时,弹簧具有的弹性势能为( )分析:求解本题的关键是明确对物体、弹簧、地面组成的系统应用能量守恒定律即可求解.
解答:解:物体受到的滑动摩擦力大小为f=μmg,对物体与弹簧及地面组成的系统,由能量守恒定律可得:
+μmg(s+x)=
,解得
=
-μmg(s+x),所以选项B正确,ACD错误.
故选:B.
| E | p |
| 1 |
| 2 |
| mv | 2 0 |
| E | p |
| 1 |
| 2 |
| mv | 2 0 |
故选:B.
点评:注意摩擦生热公式为Q=f
,其中
是物体相对接触面发生的相对路程;对系统应用能量守恒定律求解较简便.
| s | 相对 |
| s | 相对 |

练习册系列答案
相关题目
 如图所示,轻弹簧一端固定在墙上,另一端连一挡板,挡板的质量为m,一物体沿光滑水平面以一定的速度撞向挡板,物体的质量为M,物体与挡板相接触的一面都装有尼龙搭扣,使得它们相撞后立即粘连在一起,若碰撞时间极短(即极短时间内完成粘连过程),则对物体、挡板和弹簧组成的系统,下面说法中正确的是( )
如图所示,轻弹簧一端固定在墙上,另一端连一挡板,挡板的质量为m,一物体沿光滑水平面以一定的速度撞向挡板,物体的质量为M,物体与挡板相接触的一面都装有尼龙搭扣,使得它们相撞后立即粘连在一起,若碰撞时间极短(即极短时间内完成粘连过程),则对物体、挡板和弹簧组成的系统,下面说法中正确的是( ) 如图所示,轻弹簧一端固定,另一端自由伸长时恰好到达O点,将质量为m(视为质点)的物体P与弹簧连接,并将弹簧压缩到A由静止释放物体后,物体将沿水平面运动.若物体与水平面的摩擦力不能忽略,则关于物体运动的下列说法中正确的是( )
如图所示,轻弹簧一端固定,另一端自由伸长时恰好到达O点,将质量为m(视为质点)的物体P与弹簧连接,并将弹簧压缩到A由静止释放物体后,物体将沿水平面运动.若物体与水平面的摩擦力不能忽略,则关于物体运动的下列说法中正确的是( ) 如图所示,轻弹簧一端与墙相连,质量m=2kg的木块沿光滑水平面以V0=5m/s的初速度向左运动,当木块压缩弹簧后速度减为V=3m/s时弹簧的弹性势能是( )
如图所示,轻弹簧一端与墙相连,质量m=2kg的木块沿光滑水平面以V0=5m/s的初速度向左运动,当木块压缩弹簧后速度减为V=3m/s时弹簧的弹性势能是( )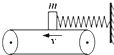 一皮带传送装置如图所示,轻弹簧一端固定,另一端连接一个质量为m的滑块,已知滑块与皮带之间存在摩擦.现将滑块轻放在皮带上,弹簧恰好处于自然长度且轴线水平.若在弹簧从自然长度到第一次达最长的过程中,滑块始终没有与皮带达到共速,则在此过程中关于滑块的运动以及速度和加速度变化的说法正确的是( )
一皮带传送装置如图所示,轻弹簧一端固定,另一端连接一个质量为m的滑块,已知滑块与皮带之间存在摩擦.现将滑块轻放在皮带上,弹簧恰好处于自然长度且轴线水平.若在弹簧从自然长度到第一次达最长的过程中,滑块始终没有与皮带达到共速,则在此过程中关于滑块的运动以及速度和加速度变化的说法正确的是( )