题目内容
6．
如图所示，置于水平地面带有竖直立杆的底座总质量为0.2kg，竖直立杆长0.5m，有一质量为0.05kg的小环从杆的下端以4m/s的初速度向上运动，刚好能到达杆的顶端，在环向上运动的过程中，底座对水平地面的压力为（ ）| A． | 1.7N | B． | 1.8N | C． | 2.0N | D． | 2.3N |
分析 小环在下落过程中，受到重力和向上的滑动摩擦力，底座受到重力、小环向下的摩擦力和地面的支持力，由平衡条件求地面对底座的支持力，即可由牛顿第三定律求得底座对地面的压力
解答 
解：根据速度-位移公式：v2=2ax
所以：Ff+mBg=mBa
FN+Ff=mAg
联立以上三式解得：FN=1.7N
由作用力和反作用力关系，底座对水平面的压力：FN′=FN=1.7N
故选：A
点评 本题中底座与小环的加速度不同，采用隔离法研究，抓住加速度是关键，由牛顿运动定律和运动学公式结合进行研究
练习册系列答案
相关题目
14．
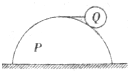如图所示，半径为R，质量为M的半球形物体P放在水平地面上，通过最高点处的钉子用水平细线拉住半径为r，质量为m的光滑球Q，P对地面压力大小为F1，P对地面的摩擦力大小为F2，细线对Q的拉力大小为F3，P对Q的支持力大小为F4，下列说法不正确的是（ ）
如图所示，半径为R，质量为M的半球形物体P放在水平地面上，通过最高点处的钉子用水平细线拉住半径为r，质量为m的光滑球Q，P对地面压力大小为F1，P对地面的摩擦力大小为F2，细线对Q的拉力大小为F3，P对Q的支持力大小为F4，下列说法不正确的是（ ）| A． | F1=（M+m）g，若增大光滑球半径r，F1一定不变 | |
| B． | 若增大光滑球的半径r，F2一定不变 | |
| C． | F3=$\frac{\sqrt{r（r+2R）}}{R}$mg，若增大光滑球半径r，F3可能减小 | |
| D． | F4=$\frac{R+r}{R}$mg，若增大光滑球半径r，F4增大 |
2．如图所示，是质量相等的两个质点A、B在同一直线上运动的v-t图象．由图可知（ ）
| A． | 在t1时刻，合外力对A做功的功率比较大 | |
| B． | 在0～t2 时间内，合外力对A，B做功的功率均匀增大 | |
| C． | 在0～t2时间内质点B比质点A位移大 | |
| D． | 在t2时刻，两质点不可能在同一位置 |
某同学用如图所示的实验装置来验证“力的平行四边形定则”．弹簧测力计A挂于固定点P，下端用细线挂一重物M．弹簧测力计B的一端用细线系于O点，手持另一端向左拉，使结点O静止在某位置．