Question

两根光滑的长直金属导轨MN、M′N′平行置于同一水平面内，导轨间距为l，电阻不计，M、M′处接有如图12-16所示的电路，电路中各电阻的阻值均为R，电容器的电容为C.长度也为l、阻值同为R的金属棒ab垂直于导轨放置，导轨处于磁感应强度为B、方向竖直向下的匀强磁场中.ab在外力作用下向右匀速运动且与导轨保持良好接触，在ab运动距离为s的过程中，整个回路中产生的焦耳热为Q.求:

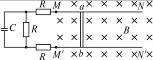
图12-16

(1)ab运动速度v的大小；

(2)电容器所带的电荷量q.

Answer 1

(1)　(2)

解析:

本题是电磁感应中的电路问题,ab切割磁感线产生感应电动势为电源.电动势可由E=Blv计算.其中v为所求,再结合闭合(或部分)电路欧姆定律、焦耳定律、电容器及运动学知识列方程可解得.

(1)设ab上产生的感应电动势为E，回路中的电流为I,ab运动距离s所用时间为t,三个电阻R与电源串联,总电阻为4R,则

E=Blv

由闭合电路欧姆定律有

由焦耳定律有Q=I²(4R)t

由上述方程得

(2)设电容器两极板间的电势差为U,则有U=IR

电容器所带电荷量q=CU

解得