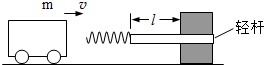
题目内容
与轻杆相连,轻杆可在固定的槽内移动,与槽间的滑动摩擦力恒为 f.轻杆向右移动不超过l时,装置可安全工作.一质量为m的小车若以速度v0撞击弹簧,将导致轻杆向右移动 l/4.轻杆与槽间的最大静擦力等于滑动摩擦力,且不计小车与地面的摩擦.

(1)若弹簧的劲度系数为k,求轻杆开始移动时,弹簧的压缩量x;
(2)求为使装置安全工作,允许该小车撞击的最大速度vm;
(3)讨论在装置安全工作时,该小车弹回速度v′和撞击速度v的关系.

(1)若弹簧的劲度系数为k,求轻杆开始移动时,弹簧的压缩量x;
(2)求为使装置安全工作,允许该小车撞击的最大速度vm;
(3)讨论在装置安全工作时,该小车弹回速度v′和撞击速度v的关系.
(1)轻杆开始移动时,弹簧的弹力F=kx ①
且F=f ②
解得 x=
③
(2)设轻杆移动前小车对弹簧所做的功为W,则小车从撞击到停止的过程中
由动能定理得
-f(
)-W=0-
m
④
同理,小车以vm撞击弹簧时-fl-W=0-
⑤
解得 vm=
⑥
(3)设轻杆恰好移动时,小车撞击速度为v1
m
=W ⑦
由④⑦解得 v1=
当v<
时,v′=v
当
≤v≤
时,
v′=
答:(1)若弹簧的劲度系数为k,轻杆开始移动时,弹簧的压缩量是
;
(2)求为使装置安全工作,允许该小车撞击的最大速度是
;
(3)该小车弹回速度v′和撞击速度v的关系是当v<
时,v′=v
当
≤v≤
时,v′=
.
且F=f ②
解得 x=
| f |
| k |
(2)设轻杆移动前小车对弹簧所做的功为W,则小车从撞击到停止的过程中
由动能定理得
-f(
| l |
| 4 |
| 1 |
| 2 |
| v | 20 |
同理,小车以vm撞击弹簧时-fl-W=0-
| 1 |
| 2 |
| v | 2m |
解得 vm=
|
(3)设轻杆恰好移动时,小车撞击速度为v1
| 1 |
| 2 |
| v | 21 |
由④⑦解得 v1=
|
当v<
|
当
|
|
v′=
|
答:(1)若弹簧的劲度系数为k,轻杆开始移动时,弹簧的压缩量是
| f |
| k |
(2)求为使装置安全工作,允许该小车撞击的最大速度是
|
(3)该小车弹回速度v′和撞击速度v的关系是当v<
|
当
|
|
|

练习册系列答案
相关题目
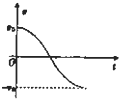
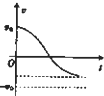
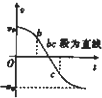
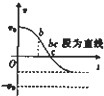
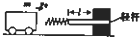 某缓冲装置的理想模型如图所示,劲度系数足够大的轻质弹簧与轻杆相连,轻杆可在固定的槽内移动,与槽间的滑动摩擦力为定值.轻杆向右移动不超过l时,装置可安全工作.若一小车以速度v0撞击弹簧,已知装置可安全工作,轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面间的摩擦.从小车与弹簧刚接触时开始计时,下列关于小车运动的速度-时间图象可能正确的是( )
某缓冲装置的理想模型如图所示,劲度系数足够大的轻质弹簧与轻杆相连,轻杆可在固定的槽内移动,与槽间的滑动摩擦力为定值.轻杆向右移动不超过l时,装置可安全工作.若一小车以速度v0撞击弹簧,已知装置可安全工作,轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面间的摩擦.从小车与弹簧刚接触时开始计时,下列关于小车运动的速度-时间图象可能正确的是( )