题目内容
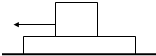 如图,长木板静止在水平桌面上,质量为m的木块在木板上水平向左滑行,木板的质量M=3m.已知木块与木板间、木板与桌面间的动摩擦因数均为μ.则木板所受桌面的摩擦力大小为
如图,长木板静止在水平桌面上,质量为m的木块在木板上水平向左滑行,木板的质量M=3m.已知木块与木板间、木板与桌面间的动摩擦因数均为μ.则木板所受桌面的摩擦力大小为
- A.μmg
- B.2μmg
- C.3μmg
- D.4μmg
A
分析:先对小滑块受力分析,受重力、长木板的支持力和向右的滑动摩擦力;再对长木板受力分析,受到重力、小滑块的对长木板向下的压力、小滑块对其向左的滑动摩擦力、地面对长木板的支持力和向右的静摩擦力;然后根据共点力平衡条件判断.
解答:对小滑块受力分析,受重力mg、长木板的支持力FN和向右的滑动摩擦力f1,有
f1=μFN
FN=mg
故f1=μmg
再对长木板受力分析,受到重力Mg、小滑块的对长木板向下的压力FN、小滑块对其向左的滑动摩擦力f1、地面对长木板的支持力FN′和向右的静摩擦力f2,根据共点力平衡条件,有
f1=f2
故f2=μmg
故选A.
点评:滑动摩擦力与正压力成正比,而静摩擦力随外力的变化而变化,故静摩擦力通常可以根据共点力平衡条件求解,或者结合运动状态,然后根据牛顿第二定律列式求解.
分析:先对小滑块受力分析,受重力、长木板的支持力和向右的滑动摩擦力;再对长木板受力分析,受到重力、小滑块的对长木板向下的压力、小滑块对其向左的滑动摩擦力、地面对长木板的支持力和向右的静摩擦力;然后根据共点力平衡条件判断.
解答:对小滑块受力分析,受重力mg、长木板的支持力FN和向右的滑动摩擦力f1,有
f1=μFN
FN=mg
故f1=μmg
再对长木板受力分析,受到重力Mg、小滑块的对长木板向下的压力FN、小滑块对其向左的滑动摩擦力f1、地面对长木板的支持力FN′和向右的静摩擦力f2,根据共点力平衡条件,有
f1=f2
故f2=μmg
故选A.
点评:滑动摩擦力与正压力成正比,而静摩擦力随外力的变化而变化,故静摩擦力通常可以根据共点力平衡条件求解,或者结合运动状态,然后根据牛顿第二定律列式求解.

练习册系列答案
相关题目
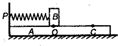 如图,木板A在水平底面上,小物块B通过轻弹簧与A的左侧挡板P连接,A与B,A与地面之间均粗糙,开始时弹簧处于原长,B位于A上的O点,现将B拉至C点由静止释放向左运动,到达某点时速度为零(上述过程中A一直保持静止),则此时( )
如图,木板A在水平底面上,小物块B通过轻弹簧与A的左侧挡板P连接,A与B,A与地面之间均粗糙,开始时弹簧处于原长,B位于A上的O点,现将B拉至C点由静止释放向左运动,到达某点时速度为零(上述过程中A一直保持静止),则此时( )| A、B所受的摩擦力可能为零 | B、A所受的摩擦力不可能为零 | C、B可能位于O点的左侧 | D、B不可能位于O点的右侧 |
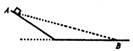
如图所示的斜板和水平板为同种材料组成,木块由斜板的顶端A点处从静止开始下滑,到达水平板上的B点时恰好静止。如果让同种材料的长木板搁置在AB两点之间(如图中虚线所示),再让木块在此木板上下滑,则木块在木板上的运动为( )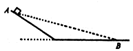
| A.匀速直线运动 | B.匀加速直线运动 |
| C.匀减速直线运动 | D.都有可能 |