题目内容
 (2013?东莞一模)如图所示,在真空中,半径为d的虚线所围的圆形区域内只存在垂直纸面向外的匀强磁场,在磁场右侧有一对平行金属板M和N,两板间距离也为d,板长为l.板
(2013?东莞一模)如图所示,在真空中,半径为d的虚线所围的圆形区域内只存在垂直纸面向外的匀强磁场,在磁场右侧有一对平行金属板M和N,两板间距离也为d,板长为l.板间存在匀强电场,两板间的电压为U0.两板的中心线O1O2,与磁场区域的圆心O在同一直线上.有一电荷量为q、质量为m的带正电粒子,以速率v0从圆周上的P点沿垂直于半径OOl并指向圆心O的方向进入磁场,从圆周上的O1点飞出磁场后沿两板的中心线O1O2射入匀强电场,从两板右端某处飞出.不计粒子所受重力.求
(1)磁场的磁感应强度B的大小
(2)粒子在磁场和电场中运动的总时间
(3)当粒子在电场中经过时间t=
| l | 2v0 |
分析:(1)粒子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,由几何知识得到轨迹半径,由牛顿第二定律求解磁感应强度的大小;
(2)粒子运动
周期时间,求得周期,即可求出粒子在磁场中运动的时间;粒子在电场中做类平抛运动,平行板的方向做匀速直线运动,而水平方向位移大小为l,由t=
求出时间,即可求出总时间;
(3)当粒子在电场中经过时间t=
时,使电场反向,要使粒子恰好能从O2点飞出电场,在前t=
时间内,粒子在竖直方向先做匀加速直线运动,再在后t=
时间内,做等时间的匀减速直线运动,两段过程竖直方向的位移大小相等、方向相反,即总位移为零,根据牛顿第二定律求出加速度,根据位移关系和位移公式求得电压U1和U0的比值.
(2)粒子运动
| 1 |
| 4 |
| l |
| v0 |
(3)当粒子在电场中经过时间t=
| l |
| 2v0 |
| l |
| 2v0 |
| l |
| 2v0 |
解答:解:(1)粒子在磁场中做匀速圆周运动,设圆周运动的半径为r,由牛顿第二定律
qv0B=m
由几何关系知 r=d
所以 B=
(2)粒子在磁场中运动的周期T=
,
在磁场中运动时间为四分之一个周期,t1=
T=
?
=
.
粒子在电场中做类平抛运动,平行板的方向做匀速直线运动
则t2=
在电磁场中运动的总时间t总=t1+t2=
(3)根据运动的独立性可知:粒子在竖直方向先做匀加速直线运动,再做等时间的匀减速直线运动,
第一阶段:a=
,s=
at2
第二阶段:a1=
,s1=vt-
a1t2=at2-
a1t2
竖直方向总位移为零,s+s1=0
所以解得 a1=3a
故U1:U0=3:1
答:(1)磁场的磁感应强度B的大小是
.
(2)粒子在磁场和电场中运动的总时间是
.
(3)电压U1和U0的比值是3:1.
qv0B=m
| ||
| r |
由几何关系知 r=d
所以 B=
| mv0 |
| qd |
(2)粒子在磁场中运动的周期T=
| 2πm |
| qB |
在磁场中运动时间为四分之一个周期,t1=
| 1 |
| 4 |
| 1 |
| 4 |
| 2πm |
| qB |
| πl |
| 2v0 |
粒子在电场中做类平抛运动,平行板的方向做匀速直线运动
则t2=
| l |
| v0 |
在电磁场中运动的总时间t总=t1+t2=
| πl+2l |
| 2v0 |
(3)根据运动的独立性可知:粒子在竖直方向先做匀加速直线运动,再做等时间的匀减速直线运动,
第一阶段:a=
| qU0 |
| md |
| 1 |
| 2 |
第二阶段:a1=
| qU1 |
| md |
| 1 |
| 2 |
| 1 |
| 2 |
竖直方向总位移为零,s+s1=0
所以解得 a1=3a
故U1:U0=3:1
答:(1)磁场的磁感应强度B的大小是
| mv0 |
| qd |
(2)粒子在磁场和电场中运动的总时间是
| πl+2l |
| 2v0 |
(3)电压U1和U0的比值是3:1.
点评:本题粒子在磁场中运动时,由几何知识求出轨迹半径是关键,在电场中分析两段位移的关系是关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
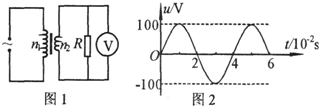 (2013?东莞一模)图l中的变压器为理想变压器,原、副线圈的匝数之比为10:1.变压器的原线圈接如图2所示的正弦交流电,电压表为理想电表接在副线圈两端.则( )
(2013?东莞一模)图l中的变压器为理想变压器,原、副线圈的匝数之比为10:1.变压器的原线圈接如图2所示的正弦交流电,电压表为理想电表接在副线圈两端.则( ) (2013?东莞一模)据央视报道,北京时间2012年10月15日凌晨,奥地利著名极限运动员鲍姆加特纳从距地面高度约3.9万米的高空跳下,并成功着陆,一举打破多项世界纪录.假设他从氦气球携带的太空舱上跳下到落地的过程中沿竖直方向运动的v-t图象如图所示,则下列说法中正确的是( )
(2013?东莞一模)据央视报道,北京时间2012年10月15日凌晨,奥地利著名极限运动员鲍姆加特纳从距地面高度约3.9万米的高空跳下,并成功着陆,一举打破多项世界纪录.假设他从氦气球携带的太空舱上跳下到落地的过程中沿竖直方向运动的v-t图象如图所示,则下列说法中正确的是( )