题目内容
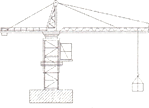
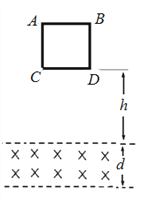
【题目】如图所示,一质量为M=2kg的木板放在光滑水平地面上,在此木板的左端上还有一质量为m=1kg的铁块。最初木板左端位于O点,现给铁块一个瞬间冲量I,当木板左端到达C点时,铁块刚好到达木板右端与木板一起运动。测得木板左端从A点运动到B点用时t1=0.2s,木板左端从B点运动到C点用时t2=0.3s;已知A、B两点间的距离是x1=0.24m,B、C两点间的距离是x2=0.51m,重力加速度g=10m/s2。求:
![]()
(1)O、A两点间的距离和铁块与木板之间的动摩擦因数;
(2)最初给铁块的瞬时冲量I的大小和木板的长度;
(3)该过程中系统产生的内能
【答案】(1)μ=0.4 (2)I=6Ns,L=3m (3)Q=12J
【解析】
(1)给铁块一个瞬间冲量I后获得了速度,在摩擦力作用下,铁块向右做匀减速运动,木板向右做匀加速运动.根据题目的条件可求得木板在AB间和BC间的平均速度,从而得到中点时刻的瞬时速度,利用加速度的定义求解木板的加速度,再由速度公式求出木板左端经过A点时的速度,由速度位移公式求出O、A两点间的距离.以木板为研究对象,由牛顿第二定律求得铁块与木板之间的动摩擦因数;
(2)根据速度公式求出铁块与木板相对静止时的共同速度。由动量守恒定律求铁块的初速度,再由动量定理求最初给铁块的瞬时冲量I的大小.以铁块为研究对象,根据牛顿第二定律和运动学公式结合求木板的长度;
(3)该过程中系统产生的内能等于μmgL.
(1)木板在A、B两点间的平均速度为:![]()
B、C两点间的平均速度为:![]()
木板匀加速运动的加速度为: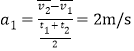
木板左端经过A点的速度为:![]()
由速度位移关系得O、A两点间的距离为:![]()
以木板为研究对象,根据牛顿第二定律得:μmg=Ma1
代入数据解得:![]()
(2)木板与铁块相对静止时的速度为:![]()
取向右为正方向,由动量守恒定律得:mv0=(m+M)vC
代入数据解得:v0=6m/s
最初给铁块的瞬时冲量为:I=mv0=1×6=6Ns
以铁块为研究对象,由牛顿第二定律得:μmg=ma2
代入数据得:a2=4m/s2
木板左端到达C点时铁块的位移为:![]()
所以木板的长度为:L=x3-(x0+x1+x2)=3m
(3)该过程中系统产生的内能为:Q=μmgL
代入数据解得:Q=12J

【题目】某同学设计了如图甲所示的电路测量某电池的电动势E和内阻r,电路中定值电阻R0=20Ω。
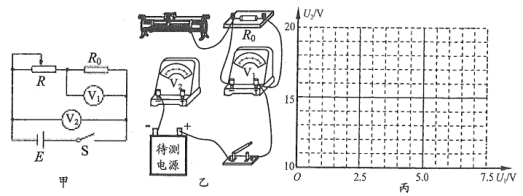
(1)根据图甲所示电路,请在图乙中用笔画线代替导线,完成实物电路的连接_______。
(2)闭合电键前,滑动变阻器滑片应置于变阻器的___________端。
(3)实验中,该同学移动滑动变阻器的滑片,读出电压表V1和V2的示数U1、U2,数据如下表所示。请根据表格中的数据在图丙所示坐标纸中画出U2-U1的图线_________。
次数 | 1 | 2 | 3 | 4 | 5 | 6 |
U1/V | 1.0 | 2.0 | 3.0 | 4.0 | 4.5 | 5.0 |
U2/V | 16.5 | 15.2 | 15.0 | 12.0 | 11.1 | 10.3 |
(4)由U2-U1图线求得该电源的电动势E=_____V,内阻r=_____Ω。(取三位有效数字)
(5)实验中,产生系统误差的主要原因是______________。