题目内容
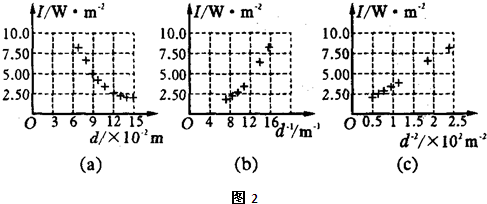
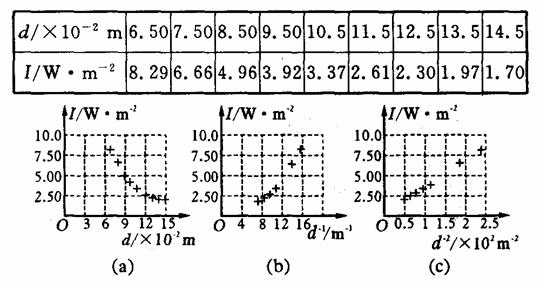
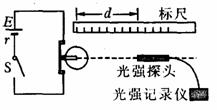
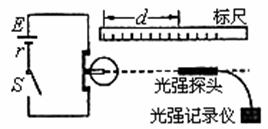
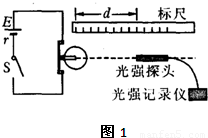
为验证小灯泡(点光源)光能的球面散射规律并测定其发光效率,有同学设计并进行了如图1所示的实验:将一个“6V 8.0W”的小灯泡接入电路,使之正常发光,在灯泡灯丝的同一水平面、正对光线方向放一个光强探头,以测定与光源间距为d时相应的光强值I,其测得以下9组数据(下表);并用一数字图象处理器将表内数据分别在I-d,I-d-1和I-d-2坐标平面内标得如下数据点,如图2所示.| d/×10-2m | 6.50 | 7.50 | 8.50 | 9.50 | 10.5 | 11.5 | 12.5 | 13.5 | 14.5 |
| I/W?m-2 | 8.29 | 6.66 | 4.96 | 3.92 | 3.37 | 2.61 | 2.30 | 1.97 | 1.70 |
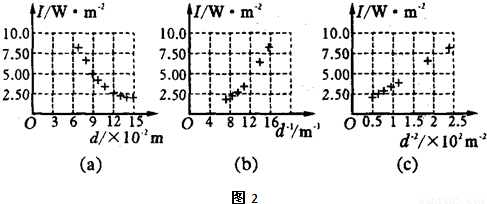
(1)根据图中三个数据点图,可看出I与哪个量存在线性关系,因此可将I与d之间的数学关系式表达为______,其中的常量为______W(保留两位有效数字).
(2)在与光源等距的各点,认为光源向各方向发出的光强大小几乎相等,依点光源光能向周围空间360球面均匀散射的物理模型,写出光源的发光功率P,光强值I及相应的与光源距离d之间的关系式______.
(3)根据以上条件,算出小电珠的电-光转换效率η=______% (保留一位有效数字).
【答案】分析:(1)找出直线,直线表示横坐标与纵坐标成正比,然后求出斜率;
(2)光强等于单位时间流过单位面积的光能,相同时间内通过各个球面的能量是相等的;
(3)将光源的发光功率除以电功率,就可以得到发光效率.
解答:解:(1)图C为直线,故光强与距离的平方成正比;
表达式为: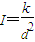
斜率为:k≈0.035W
故答案为: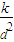 ,0.035 (0.032-0.038);
,0.035 (0.032-0.038);
(2)光强等于单位时间流过单位面积的光能,故发光功率为:
P=SI=4πd2I
故答案为:P=4πd2I.
(3)发光功率为:P=SI=4πd2I=4×3.14×(13.5×0.01)2×1.97≈0.45W
发光效率:η=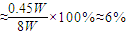
故答案为:6.
点评:本题关键明确光强的物理意义以及其定义,同时要能结合图象进行分析计算.
(2)光强等于单位时间流过单位面积的光能,相同时间内通过各个球面的能量是相等的;
(3)将光源的发光功率除以电功率,就可以得到发光效率.
解答:解:(1)图C为直线,故光强与距离的平方成正比;
表达式为:
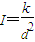
斜率为:k≈0.035W
故答案为:
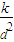 ,0.035 (0.032-0.038);
,0.035 (0.032-0.038);(2)光强等于单位时间流过单位面积的光能,故发光功率为:
P=SI=4πd2I
故答案为:P=4πd2I.
(3)发光功率为:P=SI=4πd2I=4×3.14×(13.5×0.01)2×1.97≈0.45W
发光效率:η=
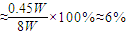
故答案为:6.
点评:本题关键明确光强的物理意义以及其定义,同时要能结合图象进行分析计算.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
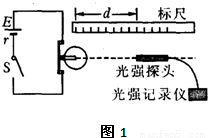
为验证小灯泡(点光源)光能的球面散射规律并测定其发光效率,有同学设计并进行了如图1所示的实验:将一个“6V 8.0W”的小灯泡接入电路,使之正常发光,在灯泡灯丝的同一水平面、正对光线方向放一个光强探头,以测定与光源间距为d时相应的光强值I,其测得以下9组数据(下表);并用一数字图象处理器将表内数据分别在I-d,I-d-1和I-d-2坐标平面内标得如下数据点,如图2所示.

(1)根据图中三个数据点图,可看出I与哪个量存在线性关系,因此可将I与d之间的数学关系式表达为______,其中的常量为______W(保留两位有效数字).
(2)在与光源等距的各点,认为光源向各方向发出的光强大小几乎相等,依点光源光能向周围空间360球面均匀散射的物理模型,写出光源的发光功率P,光强值I及相应的与光源距离d之间的关系式______.
(3)根据以上条件,算出小电珠的电-光转换效率η=______% (保留一位有效数字).
| d/×10-2m | 6.50 | 7.50 | 8.50 | 9.50 | 10.5 | 11.5 | 12.5 | 13.5 | 14.5 |
| I/W?m-2 | 8.29 | 6.66 | 4.96 | 3.92 | 3.37 | 2.61 | 2.30 | 1.97 | 1.70 |

(1)根据图中三个数据点图,可看出I与哪个量存在线性关系,因此可将I与d之间的数学关系式表达为______,其中的常量为______W(保留两位有效数字).
(2)在与光源等距的各点,认为光源向各方向发出的光强大小几乎相等,依点光源光能向周围空间360球面均匀散射的物理模型,写出光源的发光功率P,光强值I及相应的与光源距离d之间的关系式______.
(3)根据以上条件,算出小电珠的电-光转换效率η=______% (保留一位有效数字).

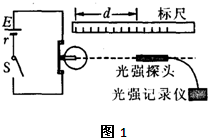 为验证小灯泡(点光源)光能的球面散射规律并测定其发光效率,有同学设计并进行了如图1所示的实验:将一个“6V 8.0W”的小灯泡接入电路,使之正常发光,在灯泡灯丝的同一水平面、正对光线方向放一个光强探头,以测定与光源间距为d时相应的光强值I,其测得以下9组数据(下表);并用一数字图象处理器将表内数据分别在I-d,I-d-1和I-d-2坐标平面内标得如下数据点,如图2所示.
为验证小灯泡(点光源)光能的球面散射规律并测定其发光效率,有同学设计并进行了如图1所示的实验:将一个“6V 8.0W”的小灯泡接入电路,使之正常发光,在灯泡灯丝的同一水平面、正对光线方向放一个光强探头,以测定与光源间距为d时相应的光强值I,其测得以下9组数据(下表);并用一数字图象处理器将表内数据分别在I-d,I-d-1和I-d-2坐标平面内标得如下数据点,如图2所示.