题目内容
17. 如图所示,质量为m、面积为S的活塞在向下开口的气缸内封闭着一定质量的理想气体.现对气缸缓慢加热,使气缸内气体温度从T1升高到T2,空气柱的高度增加了△L,已知加热时气体吸收的热量为Q,外界大气压强为P0求
如图所示,质量为m、面积为S的活塞在向下开口的气缸内封闭着一定质量的理想气体.现对气缸缓慢加热,使气缸内气体温度从T1升高到T2,空气柱的高度增加了△L,已知加热时气体吸收的热量为Q,外界大气压强为P0求(1)此过程中封闭气体的内能变化了多少?
(2)气缸内温度为T1时,气柱的长度为多少?
分析 (1)封闭气体做等压变化,根据W=P△V求出气体对外界做的功,然后根据热力学第一定律列式求解;
(2)找出初末状态参量,根据盖吕萨克定律列式求解.
解答 解:(1)对活塞根据平衡得:mg+PS=P0S
解得:$P={P}_{0}-\frac{mg}{S}$
气体对外做功:W=-P△V=PS△L=(P0S-mg)△L
有热力学第一定律得:△U=W+Q=Q-(P0S-mg)△L
(2)设气缸内温度为T1时,气柱的长度为L,温度升高过程,封闭气体做等压变化,有盖吕萨克定律得:
$\frac{LS}{{T}_{1}}=\frac{(L+△L)}{{T}_{2}}$
解得:$L=\frac{{T}_{1}△L}{{T}_{2}-{T}_{1}}$
答:(1)此过程中封闭气体的内能变化了Q-(P0S-mg)△L
(2)气缸内温度为T1时,气柱的长度为$\frac{{T}_{1}△L}{{T}_{2}-{T}_{1}}$
点评 此题较为简单,审题时注意分清气体的变化过程,利用热力学第一定律时,注意做功和热量的正负问题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
2.下列说法正确的是( )
| A. | ${\;}_{92}^{238}$U→${\;}_{90}^{234}$Th+${\;}_{2}^{4}$He是核衰变方程 | |
| B. | 10个${\;}_{92}^{238}$U原子核经过一个半衰期,必定有5个发生衰变 | |
| C. | 天然放射现象说明原子具有核式结构 | |
| D. | 波源的发射频率会随接收者的远离而降低 |
9. 图示为氢原子能级示意图.处于激发态的氢原子在跃迁中发出了a、b两种频率的光,下列说法正确的是( )
图示为氢原子能级示意图.处于激发态的氢原子在跃迁中发出了a、b两种频率的光,下列说法正确的是( )
 图示为氢原子能级示意图.处于激发态的氢原子在跃迁中发出了a、b两种频率的光,下列说法正确的是( )
图示为氢原子能级示意图.处于激发态的氢原子在跃迁中发出了a、b两种频率的光,下列说法正确的是( )| A. | 若两种光均可使一金属发生光电效应,则a光照射下金属的逸出功较大 | |
| B. | 在水中,a光传播速度小于b光 | |
| C. | 通过同一双缝干涉装置,a光的条纹间距小于b光 | |
| D. | 从水中射向真空发生全反射时,a光临界角大于b光 |
 如图所示,水平的粗糙轨道与竖直的光滑圆形轨道相连,圆形轨道间不相互重叠,即小球离开圆形轨道后可继续沿水平轨道运动.圆形轨道半径R=0.2m,右侧水平轨道BC长为L=4m,C点右侧有一壕沟,C、D两点的竖直高度h=1m,水平距离s=2m,小球与水平轨道间的动摩擦因数μ=0.2,重力加速度g=10m/s2,小球从圆形轨道最低点B以某一水平向右的初速度出发,进入圆形执道.
如图所示,水平的粗糙轨道与竖直的光滑圆形轨道相连,圆形轨道间不相互重叠,即小球离开圆形轨道后可继续沿水平轨道运动.圆形轨道半径R=0.2m,右侧水平轨道BC长为L=4m,C点右侧有一壕沟,C、D两点的竖直高度h=1m,水平距离s=2m,小球与水平轨道间的动摩擦因数μ=0.2,重力加速度g=10m/s2,小球从圆形轨道最低点B以某一水平向右的初速度出发,进入圆形执道. 一定质量的理想气体经历如图A→B→C→D→A所示循环过程,该过程每个状态视为平衡态.已知A态的温度为27℃.求:
一定质量的理想气体经历如图A→B→C→D→A所示循环过程,该过程每个状态视为平衡态.已知A态的温度为27℃.求: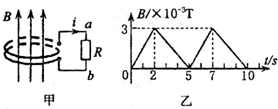 如图甲,匝数n=2的金属线圈(电阻不计)围成的面积为10cm2,线圈与R=2Ω的电阻连接,置于竖直向上、均匀分布的磁场中.磁场与线圈平面垂直,磁感应强度为B.B-t关系如图乙,规定感应电流i从a经过R到b的方向为正方向.忽略线圈的自感影响.则下列i-t关系图正确的是( )
如图甲,匝数n=2的金属线圈(电阻不计)围成的面积为10cm2,线圈与R=2Ω的电阻连接,置于竖直向上、均匀分布的磁场中.磁场与线圈平面垂直,磁感应强度为B.B-t关系如图乙,规定感应电流i从a经过R到b的方向为正方向.忽略线圈的自感影响.则下列i-t关系图正确的是( )