题目内容
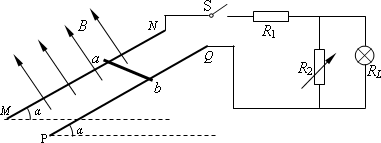
(复合场中受力+运动+恒定电流)两根相距为L的足够长的金属直角导轨如图所示放置,它们各有一边在同一水平面内,另一边垂直于水平面.质量均为m的金属细杆ab、cd与导轨垂直接触形成闭合回路,杆与水平和竖直导轨之间有相同的动摩擦因数μ,导轨电阻不计,回路总电阻为2R,整个装置处于磁感应强度大小为B、方向竖直向上的匀强磁场中.当ab杆在平行于水平导轨的拉力作用下沿导轨向右匀速运动时,cd杆也正好以某一速度向下做匀速运动,设运动过程中金属细杆ab、cd与导轨接触良好,重力加速度为g,求:

(1)ab杆匀速运动的速度v1;
(2)ab杆所受拉力F;
(3)ab杆以v1匀速运动时,cd杆以v2(v2已知)匀速运动,则在cd杆向下运动h过程中,整个回路中产生的焦耳热.
答案:
解析:
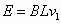 (1分)
(1分)
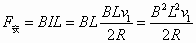 ①(2分)
①(2分)
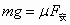 ②(2分)
②(2分)
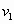 =
=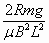 ③(1分)
③(1分)
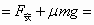
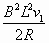 +μmg
+μmg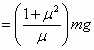 ④(3分)
④(3分)
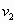 速度向下运动
速度向下运动 过程中,ab杆匀速运动了
过程中,ab杆匀速运动了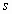 距离,
距离,
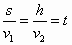 ,∴
,∴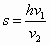 (2分)
(2分)
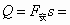
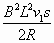 =
=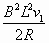
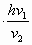 =
=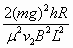 (2分)
(2分)
解析:
解:
(1)ab杆向右运动时,ab杆中产生的感应电动势方向为a→b,大小为
cd杆中的感应电流方向为d→c,cd杆受到的安培力方向水平向右
安培力大小为
cd杆向下匀速运动,有
解
①、②两式,ab杆匀速运动的速度为(2)ab杆所受拉力F
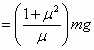 ④(3分)
④(3分)
(3)设cd杆以
整个回路中产生的焦耳热等于克服安培力所做的功

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目