题目内容
(2005?北京)下雪天,卡车在笔直的高速公路上匀速行驶.司机突然发现前方停着一辆故障车,他将刹车踩到底,车轮被抱死,但卡车仍向前滑行,并撞上故障车,且推着它共同滑行了一段距离l后停下.事故发生后,经测量,卡车刹车时与故障车距离为L,撞车后共同滑行的距离l=
L.假定两车轮胎与雪地之间的动摩擦因数相同.已知卡车质量M为故障车质量m的4倍.
(1)设卡车与故障车相撞前的速度为v1,两车相撞后的速度变为v2,求
(2)卡车司机至少在距故障车多远处采取同样的紧急刹车措施,事故就能免于发生.
| 8 |
| 25 |
(1)设卡车与故障车相撞前的速度为v1,两车相撞后的速度变为v2,求
| v1 |
| v2 |
(2)卡车司机至少在距故障车多远处采取同样的紧急刹车措施,事故就能免于发生.
分析:根据动量守恒定律求出两车相撞后的速度.
清楚碰撞前后运动过程分析,运用动能定理研究相撞前卡车和碰撞后两车得出关系式.
清楚碰撞前后运动过程分析,运用动能定理研究相撞前卡车和碰撞后两车得出关系式.
解答:解:(1)由碰撞过程动量守恒Mv1=(M十m)v2 ①
则
=
2)设卡车刹车前速度为v0,轮胎与雪地之间的动摩擦因数为μ,根据动能定理得:
两车相撞前卡车动能变化
Mv02-
Mv12=μMgL ②
碰撞后两车共同向前滑动,动能变化
(m+M)v22-0=μ(m+M)gl ③
由②式 v02-v12=2μgL
由③式 v22=2μgl
又因l=
L,得 v02=3μgl
如果卡车滑到故障车前便停止,由
Mv02=μMgL′④
解得:L′=
L
这意味着卡车在距故障前至少
L处便紧急刹车,才能免于事故.
答:(1)设卡车与故障车相撞前的速度为v1,两车相撞后的速度变为v2,
=
,
(2)卡车在距故障前至少
L处便紧急刹车,才能免于事故.
则
| v1 |
| v2 |
| 5 |
| 4 |
2)设卡车刹车前速度为v0,轮胎与雪地之间的动摩擦因数为μ,根据动能定理得:
两车相撞前卡车动能变化
| 1 |
| 2 |
| 1 |
| 2 |
碰撞后两车共同向前滑动,动能变化
| 1 |
| 2 |
由②式 v02-v12=2μgL
由③式 v22=2μgl
又因l=
| 8 |
| 25 |
如果卡车滑到故障车前便停止,由
| 1 |
| 2 |
解得:L′=
| 3 |
| 2 |
这意味着卡车在距故障前至少
| 3 |
| 2 |
答:(1)设卡车与故障车相撞前的速度为v1,两车相撞后的速度变为v2,
| v1 |
| v2 |
| 5 |
| 4 |
(2)卡车在距故障前至少
| 3 |
| 2 |
点评:碰撞的瞬间我们可以运用动量守恒定律研究问题.
该题可以运用动能定理也可以运用运动学公式解决问题.
该题可以运用动能定理也可以运用运动学公式解决问题.

练习册系列答案
相关题目
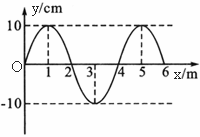
 (2005?北京)一列简谐机械横波某时刻的波形图如图所示,波源的平衡位置坐标为x=0.当波源质点处于其平衡位置上方且向下运动时,介质中平衡位置坐标x=2m的质点所处位置及运动情况是( )
(2005?北京)一列简谐机械横波某时刻的波形图如图所示,波源的平衡位置坐标为x=0.当波源质点处于其平衡位置上方且向下运动时,介质中平衡位置坐标x=2m的质点所处位置及运动情况是( ) (2005?北京)如图,一个盛水的容器底部有一小孔.静止时用手指堵住小孔不让它漏水,假设容器在下述几种运动过程中始终保持平动,且忽略空气阻力,则( )
(2005?北京)如图,一个盛水的容器底部有一小孔.静止时用手指堵住小孔不让它漏水,假设容器在下述几种运动过程中始终保持平动,且忽略空气阻力,则( ) (2005?北京)现将电池组、滑线变阻器、带铁芯的线圈A、线圈B、电流计及开关如图连接,在开关闭合、线圈A放在线圈B中的情况下,某同学发现当他将滑线变阻器的滑动端P向左加速滑动时,电流计指针向右偏转.由此可以判断( )
(2005?北京)现将电池组、滑线变阻器、带铁芯的线圈A、线圈B、电流计及开关如图连接,在开关闭合、线圈A放在线圈B中的情况下,某同学发现当他将滑线变阻器的滑动端P向左加速滑动时,电流计指针向右偏转.由此可以判断( )