��Ŀ����
2����ͼ����ʾ��PΪ����Բ�����뾶r=5m�����ڵĴų���ʱ��仯��ͼ����ͼ����ʾ���Դ�ֱֽ������Ϊ�ų�������A��B�Ǵ���С�Ĵ�������壬UAB=100V��C��D����P��������ˮƽ���õ�ƽ�н����壬�峤L=16m��������D=16m��Q�DZ߳�d=24m�������δų�����P��Բ�ģ�A��B��С�����ߣ�C��D������������Q�����߶���ͬһ��ˮƽ���ϣ���������m=1��10-4kg������q=+1.6��10-5C�����ӣ��������ƣ�ԴԴ���ϵĴ�A��С���ɾ�ֹ�ͷţ����ν���C��D���弰�����δų�������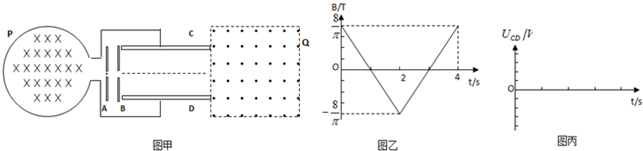
��1�����������뿪A��B�����C��D��ʱ���ٶ�v��
��2����ͼ��������C��D�������ϵĵ��Ʋ�UCD��ʱ��仯��ͼ��
��3���������Ӵ�ԽC��D������в��������ƫתλ��Y1����Сƫתλ��Y2��
��4����ʹ��������ȫ���������δų����±߽�������Ÿ�Ӧǿ�ȴ�СӦ������ʲô������
���� ��1�����������ڵ糡���������˶����糡���������ɶ��ܶ�����������ٶȣ�
��2������CD֮��ĵ��Ʋ����Բ���ڲ����ĸ�Ӧ�綯�ƣ��ɷ����ڵ�Ÿ�Ӧ���ɼ��������
��3�����������ڼ���CD֮�䷢��ƫת�����˶���ˮƽ��������ֱ����ֽ⼴�ɣ�
��4�������������糡����ٶȣ��ڴų��У������������ṩ������������ӵİ뾶��Ȼ�������Ӿʹų�ʱ�ĽǶȣ�ͨ����ͼ�ó��ٽ�������Ȼ���ٽ�ϼ��ι�ϵ��ȽϹ�ʽ���������
��� �⣺��1�����������ڵ糡���������˶����糡���������ɶ��ܶ����ã�$q{U}_{AB}=\frac{1}{2}m{v}_{0}^{2}$
���ԣ�${v}_{0}=\sqrt{\frac{2q{U}_{AB}}{m}}=\sqrt{\frac{2��1.6��1{0}^{-5}��100}{1��1{0}^{-4}}}$=4$\sqrt{2}$m/s
��2��Բ���ڲ����ĸ�Ӧ�綯�ƣ��ɷ����ڵ�Ÿ�Ӧ���ɵã�$E=\frac{����}{��t}=\frac{��B}{��t}•S=\frac{\frac{8}{��}-0}{1}���С�{5}^{2}$=200V
P�еĴų��ķ���ʼʱ�����С������ζ��ɿ�֪��Ӧ�綯�Ƶķ���Ϊ˳ʱ�뷽������C����ĵ��Ƹߣ�
����CD֮��ĵ��Ʋ����Բ���ڲ����ĸ�Ӧ�綯�Ƽ���UCD=E=200V
���ų��ı仯�ʵķ������仯������ζ��ɿ�֪����Ӧ�綯�Ƶķ����෴�����ԣ�UCD��=-E=-200V
����CD֮��ĵ��Ʋ���ʱ��ı仯��ϵ��ͼ��
��3�����������ڼ���CD֮�䷢��ƫת����ˮƽ����L=v0t
���ԣ�t=$\frac{L}{{v}_{0}}=\frac{16}{4\sqrt{2}}=2\sqrt{2}$s
�����ڵ糡�еļ��ٶȣ�$a=\frac{F}{m}=\frac{qE}{m}=\frac{q{U}_{CD}}{mD}=\frac{1.6��1{0}^{-5}��200}{1��1{0}^{-4}��16}$=$\sqrt{2}$m/s2
����ɿ�ʼ���ܵ��ĵ糡���ķ������£��������������˶���2s�������������˶������Լ��ٵ�ʱ��Խ�����������ڵ糡�е�λ��Խ��
�������ڵ糡�п�ʼʱ���ٵ�ʱ��Ƚ϶̣������ڵ糡�������¼��٣�һ��ʱ������¼��٣���������ϼ��٣�������һ���������������ӵ�ƫת������ǡ�õ���0��
1����������t=0ʱ����糡������ٵ�ʱ����2s���ص糡�����ĩ�ٶȣ�${v}_{y}=a•t��=\sqrt{2}��2=2\sqrt{2}$m/s
�����ص糡�����λ�ƣ�${x}_{1}=\frac{1}{2}at{��}^{2}=\frac{1}{2}��\sqrt{2}��{2}^{2}=2\sqrt{2}$m
�˺����������������˶���λ�ƣ�${x}_{2}={v}_{y}��t-t�䣩-\frac{1}{2}a��t-t�䣩^{2}$=$2\sqrt{2}����2\sqrt{2}-2��-\frac{1}{2}��\sqrt{2}��{��2\sqrt{2}-2��}^{2}$=$16-10\sqrt{2}$m
�������λ�ƣ�${Y}_{1}={x}_{1}+{x}_{2}=2\sqrt{2}+��16-10\sqrt{2}��=16-8\sqrt{2}$m
������ǡ����t=2sʱ����糡�У�������һֱ�����˶������������˶�����Сλ��һ����0��
��4�����Ӵ����磬�������εĴų������ڵĴų��ķ������⣬�����ֶ����֪������ƫת�ķ������£����������ص糡�߷������µķ��ٶ�Խ�����µ�λ��Խ����������Խ���״������δų����±߽�����������ϵķ��ٶ�Խ���ڵ糡�����ϵ�λ��Խ����Խ�����״������δų����±߽��������������ǡ����t=2sʱ����糡�У�������һֱ�����˶�ʱ����������״������δų����±߽������
ǡ����t=2sʱ����糡�����ӵ����ϵ�λ�ƣ�${x}_{3}=\frac{1}{2}at{��}^{2}=\frac{1}{2}��\sqrt{2}��{��4-2��}^{2}=2\sqrt{2}$m
������ֱ���ϵķ��ٶȣ�${v}_{y}��=a•t��=\sqrt{2}����4-2��=2\sqrt{2}$m/s
�����ٶȵķ�����ˮƽ����֮��ļнǣ�$tan��=\frac{{v}_{y}}{{v}_{0}}=\frac{2\sqrt{2}}{4\sqrt{2}}=\frac{1}{2}$�����ԣ���=30��
������Ӿʹų�ʱ�ĽǶȣ���ͼ��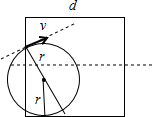
��ͼ�еļ��ι�ϵ�ã�$r+rcos30��=\frac{d}{2}+{x}_{3}$
���ӵ��ٶȣ�$v=\sqrt{{v}_{0}^{2}{+v}_{y}^{2}}$=$2\sqrt{5}$m/s
�ڴų��У������������ṩ�������ã�$qvB=\frac{m{v}^{2}}{r}$
���ӵİ뾶��$r=\frac{mv}{qB}=\frac{1��1{0}^{-4}��2\sqrt{5}}{1.6��1{0}^{-5}��B}=\frac{25\sqrt{5}}{2B}$��
������ã�$B=\frac{50\sqrt{5}+25\sqrt{15}}{48+8\sqrt{2}}$
���ڴŸ�Ӧǿ��Խ���������˶��İ뾶Ҳ��ԽС��������ʹ��������ȫ���������δų����±߽�������Ÿ�Ӧǿ�ȴ�СӦ������$B��\frac{50\sqrt{5}+25\sqrt{15}}{48+8\sqrt{2}}$
�𣺣�1�����������뿪A��B�����C��D��ʱ���ٶ���$4\sqrt{2}$m/s��
��2����ͼ��������C��D�������ϵĵ��Ʋ�UCD��ʱ��仯��ͼ����ͼ1��
��3���������Ӵ�ԽC��D������в��������ƫתλ����$16-8\sqrt{2}$m����Сƫתλ����0��
��4����ʹ��������ȫ���������δų����±߽�������Ÿ�Ӧǿ�ȴ�СӦ������$B��\frac{50\sqrt{5}+25\sqrt{15}}{48+8\sqrt{2}}$��
���� ���⽫���������ڵ糡�еļ������⡢ƫת��������������ڴų��е��˶��Լ������ڵ�Ÿ�Ӧ�������ϣ��ۺϿ���糡���ų��Լ���Ÿ�Ӧ���ɣ��ǿ����Ÿ�Ӧ�����бȽ��ټ��������Ҳ�Ǵ������ӲŴų����˶�����Ŀ���ټ�����������Ҹ����е�����ʼ�մ��и��ţ��ڼ���Ĺ�����ҲҪϸ�ģ�

 ��У����ϵ�д�
��У����ϵ�д�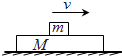 ��ͼ��ʾ������Ϊm��ľ���������ΪM��ľ���ϣ�һ��������һ��У�ľ�������䶯Ħ������Ϊ��1��ľ����ľ��䶯Ħ������Ϊ��2��ľ����ľ����Ծ�ֹ��ľ���ܵ������Ħ����Ϊf1��ľ���ܵ�ľ���Ħ����Ϊf2��������
��ͼ��ʾ������Ϊm��ľ���������ΪM��ľ���ϣ�һ��������һ��У�ľ�������䶯Ħ������Ϊ��1��ľ����ľ��䶯Ħ������Ϊ��2��ľ����ľ����Ծ�ֹ��ľ���ܵ������Ħ����Ϊf1��ľ���ܵ�ľ���Ħ����Ϊf2��������| A�� | f1=��1 Mg f2=��1 mg | B�� | f1=��1��M+m��g f2=��1 mg | ||
| C�� | f1=��1Mg f2=��2mg | D�� | f1=��1��M+m��g f2=��2 mg |
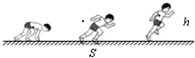 ij�˶�Ա�μӰ������ܣ������ö�ʽ���ܣ��ڷ���ǹ������Ѹ�ٵ���������������ǰ���ٵ�ͬʱ�����������ģ���ͼ��ʾ����������Ϊm���˶�Ա��������ʱǰ���ľ���S�ڣ�����������Ϊh����õ��ٶ�Ϊv����������ΪW�������ڴ˹����У�������
ij�˶�Ա�μӰ������ܣ������ö�ʽ���ܣ��ڷ���ǹ������Ѹ�ٵ���������������ǰ���ٵ�ͬʱ�����������ģ���ͼ��ʾ����������Ϊm���˶�Ա��������ʱǰ���ľ���S�ڣ�����������Ϊh����õ��ٶ�Ϊv����������ΪW�������ڴ˹����У�������| A�� | �˶�Ա�Ļ�е��������$\frac{1}{2}$mv2 | |
| B�� | �˶�Ա�Ļ�е��������$\frac{1}{2}$mv2+mgh | |
| C�� | �˶�Ա����������ΪW��=mgh | |
| D�� | �˶�Ա��������W��=$\frac{1}{2}$mv2+mgh-W�� |
 ��ͼ��ʾ������ΪG��ij����Ա��ֹ����ֱ����ǽ��֮�䣬������Ա���ȳ���ǽ��֮��Ŀ���֮��Ϊ5��8��ǽ�ڶ�ÿ���ȵ���������ǡ�������ȷ�����ǽ�ڶ�ÿ���ȵĵ�����СΪ��������
��ͼ��ʾ������ΪG��ij����Ա��ֹ����ֱ����ǽ��֮�䣬������Ա���ȳ���ǽ��֮��Ŀ���֮��Ϊ5��8��ǽ�ڶ�ÿ���ȵ���������ǡ�������ȷ�����ǽ�ڶ�ÿ���ȵĵ�����СΪ��������| A�� | $\frac{2G}{3}$ | B�� | $\frac{3G}{4}$ | C�� | $\frac{4G}{5}$ | D�� | $\frac{5G}{6}$ |
| A�� | ������ܶ����� | B�� | ������ӵ�ƽ���������� | ||
| C�� | ���û�ж��������� | D�� | ������������������ |
 ��ֱ����Դ�����費�ƣ��������䡢����˫�����ء��������ɣ�����ͼ��ʾ�ĵ�·�ϣ���ɲ���õ��ֱ��2.5V������RV��ʵ�飮�ڲ���ж��·������£������ز�����
��ֱ����Դ�����費�ƣ��������䡢����˫�����ء��������ɣ�����ͼ��ʾ�ĵ�·�ϣ���ɲ���õ��ֱ��2.5V������RV��ʵ�飮�ڲ���ж��·������£������ز����� ��ͼ��ʾ��һС����һ�뾶ΪR����ֱ�⻬Բ������˶���������͵�Aʱ�ܵ�����ĵ���ΪF1��������ߵ�Bʱ�ܵ�����ĵ���ΪF2���������ٶ�Ϊg����С����A���B��Ķ���EK1��EK2��С�������m��
��ͼ��ʾ��һС����һ�뾶ΪR����ֱ�⻬Բ������˶���������͵�Aʱ�ܵ�����ĵ���ΪF1��������ߵ�Bʱ�ܵ�����ĵ���ΪF2���������ٶ�Ϊg����С����A���B��Ķ���EK1��EK2��С�������m�� ��ͼ��ʾ������ϵxOy����ֱƽ���ڣ�x����ˮƽ����x��0�������д�ֱ������ƽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB1����������ͬʱ�����Ŵ�ֱ������ƽ���������ǿ�ų�����ֱ���ϵ���ǿ�糡���Ÿ�Ӧǿ�ȴ�СΪB2���糡ǿ�ȴ�СΪE��x��0������̶�һ��x��ɦ�=30��ǵľ�Եϸ�ˣ�һ����ϸ���ϵĴ���С��a��ϸ�����ٻ��£���N��ǡ����Բ�ܹ���˶���x���ϵ�Q�㣬���ٶȷ���ֱ��x�ᣮ��֪Q�㵽����ԭ��O�ľ���Ϊ$\frac{3}{2}$l���������ٶ�Ϊg��B1=7E$\sqrt{\frac{1}{10��gl}}$��B2=E$\sqrt{\frac{5��}{6gl}}$�������������Բ��ƣ���
��ͼ��ʾ������ϵxOy����ֱƽ���ڣ�x����ˮƽ����x��0�������д�ֱ������ƽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB1����������ͬʱ�����Ŵ�ֱ������ƽ���������ǿ�ų�����ֱ���ϵ���ǿ�糡���Ÿ�Ӧǿ�ȴ�СΪB2���糡ǿ�ȴ�СΪE��x��0������̶�һ��x��ɦ�=30��ǵľ�Եϸ�ˣ�һ����ϸ���ϵĴ���С��a��ϸ�����ٻ��£���N��ǡ����Բ�ܹ���˶���x���ϵ�Q�㣬���ٶȷ���ֱ��x�ᣮ��֪Q�㵽����ԭ��O�ľ���Ϊ$\frac{3}{2}$l���������ٶ�Ϊg��B1=7E$\sqrt{\frac{1}{10��gl}}$��B2=E$\sqrt{\frac{5��}{6gl}}$�������������Բ��ƣ���