题目内容
如右图所示，位于竖直平面内的固定光滑圆环轨道与水平面 相切于M点，与竖直墙相切于A点，竖直墙上另一点B与M的连线和水平面的夹角为600，C是圆环轨道的圆心。已知在同一时刻：a、b两球分别由A、B两点从静止开始沿光滑倾斜直轨道分别AM、BM运动到M点；c球由C点自由下落到M点；则：（ ）
A．a球最先到达M点
B．b球最先到达M点
C．c球最先到达M点
D．b球和c球都可能最先到达M点
C
解析试题分析：由题可知A、B、C三球均做初速度为零的匀加速直线运动，有匀变速直线运动的位移公式可得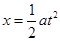
， 
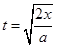，由题可得
、
、
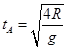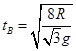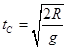可见c球最先到达M点。
故选C
考点：牛顿第二定律
点评：关键是准确得出各小球运动的位移与加速度，由位移公式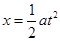求解。
练习册系列答案
相关题目
如右图所示，位于竖直平面内的固定光滑圆环轨道与水平面相切于M点，与竖直墙相切于A点，竖直墙上另一点B与M的连线和水平面的夹角为60°，C是圆环轨道的圆心，D是圆环上与M靠得很近的一点（弧长DM远小于圆环半径）．已知在同一时刻：a、b两球分别由A、B两点从静止开始沿光滑倾斜直轨道运动到M点；c球由C点自由下落到M点；d球从D点静止出发沿圆环运动到M点．则（ ）| A、a球比b球先到达M点 | B、b球最先到达M点 | C、c球最先到达M点 | D、a球与d球同时到达M点 |
