题目内容
12. 如图所示,PQS、MNE是两根足够长的固定平行金属导轨,由倾斜与水平两部分平滑连接而成,两导轨间的距离为L,倾斜导轨PQ、MN光滑且与水平面的夹角为θ,水平导轨QS、NE粗糙.在整个导轨平面内都有方向如图的竖直的匀强磁场,磁感强度大小均为B,在导轨的M、P端连接一个阻值为R的电阻.金属棒ab垂直于导轨放置且静止不动,电阻为R,质量为m;cd棒电阻为r,质量为M,在拉力作用下在水平轨道上匀速运动,cd与水平轨道间的动摩擦因数为μ,求:
如图所示,PQS、MNE是两根足够长的固定平行金属导轨,由倾斜与水平两部分平滑连接而成,两导轨间的距离为L,倾斜导轨PQ、MN光滑且与水平面的夹角为θ,水平导轨QS、NE粗糙.在整个导轨平面内都有方向如图的竖直的匀强磁场,磁感强度大小均为B,在导轨的M、P端连接一个阻值为R的电阻.金属棒ab垂直于导轨放置且静止不动,电阻为R,质量为m;cd棒电阻为r,质量为M,在拉力作用下在水平轨道上匀速运动,cd与水平轨道间的动摩擦因数为μ,求:(1)cd棒中电流的大小和方向;
(2)cd棒匀速运动的速度的大小和方向;
(3)当流过cd棒电量为q时,cd棒运动的位移的大小x?
分析 (1)以ab棒为研究对象,根据平衡条件和安培力公式结合,求解电流的大小和方向.
(2)由欧姆定律求出cd棒产生的感应电动势,再由E=BLv求cd棒匀速运动的速度的大小,由右手定则判断其速度方向.
(3)电量等于电流与时间的乘积,根据电流与x的关系求解.
解答 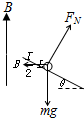 解:(1)设cd棒中电流的大小为I.
解:(1)设cd棒中电流的大小为I.
以ab棒为研究对象,其受力情况如图.
由平衡条件得:
$B\frac{I}{2}Lcosθ=mgsinθ$
得 $I=\frac{2mg}{BL}tanθ$
由左手定则判断知方向由d到c.
(2)cd棒产生的感应电动势为 $E=I(\frac{R}{2}+r)$
又 E=BLv,得 $v=\frac{mg(R+2r)}{{{B^2}{L^2}}}tanθ$
由右手定则知cd棒的速度方向水平向右.
(3)过cd棒的电量 q=I△t,x=v△t,得 $x=\frac{q}{BL}(\frac{R}{2}+r)$
答:
(1)cd棒中电流的大小为$\frac{2mg}{BL}tanθ$,方向由d到c;
(2)cd棒匀速运动的速度的大小为$\frac{mg(R+2r)}{{B}^{2}{L}^{2}}tanθ$,方向水平向右;
(3)当流过cd棒电量为q时,cd棒运动的位移的大小x为$\frac{q}{BL}(\frac{R}{2}+r)$.
点评 本题是双杆问题,要根据两杆的状态,运用力学规律和电磁感应知识处理,运用左手定则和右手定则时要注意条件、方法的不同,不要混淆.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
2.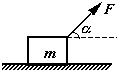 如图所示,质量为m的木箱在与水平面成θ的推力F作用下,在水平地面上滑行,已知木箱与地面间的动摩擦因数为μ,那物体受到的滑动摩擦力大小为( )
如图所示,质量为m的木箱在与水平面成θ的推力F作用下,在水平地面上滑行,已知木箱与地面间的动摩擦因数为μ,那物体受到的滑动摩擦力大小为( )
 如图所示,质量为m的木箱在与水平面成θ的推力F作用下,在水平地面上滑行,已知木箱与地面间的动摩擦因数为μ,那物体受到的滑动摩擦力大小为( )
如图所示,质量为m的木箱在与水平面成θ的推力F作用下,在水平地面上滑行,已知木箱与地面间的动摩擦因数为μ,那物体受到的滑动摩擦力大小为( )| A. | μ mg | B. | μ (mg-Fsinθ) | C. | Fcosθ | D. | μ(mg+Fcosθ) |
3.若一个负电荷仅受电场力作用,从电场中的A点运动到B点,在此过程中该电荷做初速度为零的匀加速直线运动,则A、B两点电场强度EA、EB及该电荷在A、B两点的电势能EPA、EPB之间的关系为( )
| A. | EA=EB | B. | EA>EB | C. | EPA=EPB | D. | EPA<EPB |
7.一个物体从静止开始做匀变速直线运动,下面有四种说法,正确的是( )
| A. | 前1s内,前2s内,前3s内…相应的运动距离之比一定是x1:x2:x3:…=1:4:9:… | |
| B. | 第1s内、第2s内、第3s内…相邻的相同时间内的位移之比一定是xⅠ:xⅡ:xⅢ:…=1:3:5:… | |
| C. | 相邻的相同时间内位移之差值一定是△x=aT2,其中T为相同的时间间隔 | |
| D. | 通过连续相同位移的末速度之比是:v1:v2:v3:…=1:2:3:… |
17.在水平面上有a、b两点,相距20cm,一质点在一恒定的合外力作用下沿a向b做直线运动,经过0.2s的时间先后通过a、b两点,则该质点通过a、b中点时的速度大小为( )
| A. | 无论力的方向如何均大于1 m/s | |
| B. | 无论力的方向如何均小于1 m/s | |
| C. | 若力的方向由a向b,则大于1 m/s,若力的方向由b向a,则小于1 m/s | |
| D. | 若力的方向由a向b,则小于1 m/s,若力的方向由b向a,则大于1 m/s |
4.在观察布朗运动时,下面说法正确的是( )
| A. | 布朗运动是指悬浮液体中的固体分子的运动 | |
| B. | 布朗运动是指液体分子的运动 | |
| C. | 布朗运动是液体分子运动的反映 | |
| D. | 液体的温度越低,布朗运动越显著 |
 图为接在50Hz低压交流电源上的打点计时器在纸带做匀加速直线运动时打出的一列点,图中所标的是每隔5个点所取的记数点,但第3个记数点M没有画出,则该物体运动的加速度为0.51m/s2,BM间的距离约为0.044m.
图为接在50Hz低压交流电源上的打点计时器在纸带做匀加速直线运动时打出的一列点,图中所标的是每隔5个点所取的记数点,但第3个记数点M没有画出,则该物体运动的加速度为0.51m/s2,BM间的距离约为0.044m. 实验室的游标卡尺存在零误差,当把测量尺完全合拢对齐时,主尺和游标尺上的零刻度未对齐.如图甲,两个刻度尺之间的距离为0.35mm,则该游标卡尺测量某物体长度时,如图乙所示,则该物体的真实长度为13.70mm.
实验室的游标卡尺存在零误差,当把测量尺完全合拢对齐时,主尺和游标尺上的零刻度未对齐.如图甲,两个刻度尺之间的距离为0.35mm,则该游标卡尺测量某物体长度时,如图乙所示,则该物体的真实长度为13.70mm. 如图所示,地面上方竖直界面N左侧空间存在着水平的、垂直纸面向里的匀强磁场,磁感应强度B=2.0T.与N平行的竖直界面M左侧存在竖直向下的匀强电场,电场强度E1=100N/C.在界面M与N之间还同时存在着水平向左的匀强电场,电场强度E2=100N/C.在紧靠界面M处有一个固定在水平地面上的竖直绝缘支架,支架上表面光滑,支架上放有质量m2=1.8×10-4kg的带正电的小物体b(可视为质点),电荷量q2=1.0×10-5 C.一个质量为m1=1.8×10-4 kg,电荷量为q1=3.0×10-5 C的带负电小物体(可视为质点)a以水平速度v0射入场区,沿直线运动并与小物体b相碰,a、b两个小物体碰后粘合在一起成小物体c,进入界面M右侧的场区,并从场区右边界N射出,落到地面上的Q点(图中未画出).已知支架顶端距地面的高度h=1.0m,M和N两个界面的距离L=0.10m,g取10m/s2.求:
如图所示,地面上方竖直界面N左侧空间存在着水平的、垂直纸面向里的匀强磁场,磁感应强度B=2.0T.与N平行的竖直界面M左侧存在竖直向下的匀强电场,电场强度E1=100N/C.在界面M与N之间还同时存在着水平向左的匀强电场,电场强度E2=100N/C.在紧靠界面M处有一个固定在水平地面上的竖直绝缘支架,支架上表面光滑,支架上放有质量m2=1.8×10-4kg的带正电的小物体b(可视为质点),电荷量q2=1.0×10-5 C.一个质量为m1=1.8×10-4 kg,电荷量为q1=3.0×10-5 C的带负电小物体(可视为质点)a以水平速度v0射入场区,沿直线运动并与小物体b相碰,a、b两个小物体碰后粘合在一起成小物体c,进入界面M右侧的场区,并从场区右边界N射出,落到地面上的Q点(图中未画出).已知支架顶端距地面的高度h=1.0m,M和N两个界面的距离L=0.10m,g取10m/s2.求: