题目内容
质量为m=2kg的质点停在一平面直角坐标系xOy的原点O,它受到三个力的作用,正好在O点处于静止状态,已知三个力都在xOy平面内,且其中的F2=4N,方向沿y轴的负方向,从t=0时起,停止其中F1的作用,到第2s末质点的位置坐标为(-2m,0),求:
(1)F1的大小和方向;
(2)若从第2s末起恢复F1的作用,而同时停止第三个力F3的作用,则到第4s末质点的坐标位置是多少?
(3)第4s末质点的速度大小和方向如何?
(1)F1的大小和方向;
(2)若从第2s末起恢复F1的作用,而同时停止第三个力F3的作用,则到第4s末质点的坐标位置是多少?
(3)第4s末质点的速度大小和方向如何?
(1)根据匀加速直线运动位移公式得:s=
a1t2
解得:a1=
=
m/s2=1 m/s2
根据牛顿第二定律得:F1=ma=2 N,方向:沿x轴正方向
(2)第2 s末质点的速度:v1=-at=-2 m/s
沿x轴方向:a1=1 m/s2
沿y轴方向:a2=
=2 m/s2
x=-x0+v1t+
a1t2=(-2-2×2+
×1×22)m=-4 m
y=-
a2t2=-
×2×22 m=-4 m
所以第4 s未质点的位置坐标为(-4 m,-4 m)
(3)沿x方向速度:vx=v1+a1t=(-2+1×2)m/s=0
沿y方向速度:vy=-a2t=-2×2 m/s=-4 m/s
∴第4 s末速度:v4=4 m/s,方向沿y轴负方向
答:(1)F1的大小为2 N,沿x轴正方向;
(2)第4s末质点的坐标位置是(-4 m,-4 m);
(3)第4s末质点的速度大小为4 m/s,方向沿y轴负方向.
| 1 |
| 2 |
解得:a1=
| 2s |
| t2 |
| 2×2 |
| 2×2 |
根据牛顿第二定律得:F1=ma=2 N,方向:沿x轴正方向
(2)第2 s末质点的速度:v1=-at=-2 m/s
沿x轴方向:a1=1 m/s2
沿y轴方向:a2=
| F2 |
| m |
x=-x0+v1t+
| 1 |
| 2 |
| 1 |
| 2 |
y=-
| 1 |
| 2 |
| 1 |
| 2 |
所以第4 s未质点的位置坐标为(-4 m,-4 m)
(3)沿x方向速度:vx=v1+a1t=(-2+1×2)m/s=0
沿y方向速度:vy=-a2t=-2×2 m/s=-4 m/s
∴第4 s末速度:v4=4 m/s,方向沿y轴负方向
答:(1)F1的大小为2 N,沿x轴正方向;
(2)第4s末质点的坐标位置是(-4 m,-4 m);
(3)第4s末质点的速度大小为4 m/s,方向沿y轴负方向.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
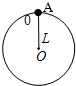 长度为L=0.4m的轻质细杆OA,A端连有一质量为m=2kg的小球,如图所示,小球以O点为圆心在竖直平面内做圆周运动,通过最高点时小球的速率是1m/s,则此时细杆对小球的作用力为( )
长度为L=0.4m的轻质细杆OA,A端连有一质量为m=2kg的小球,如图所示,小球以O点为圆心在竖直平面内做圆周运动,通过最高点时小球的速率是1m/s,则此时细杆对小球的作用力为( )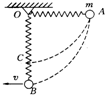 如图所示,质量为m=2kg的小球系在轻质弹簧的一端,另一端固定在悬点O处,将弹簧拉至水平位置A处,且弹簧处于自然状态,弹簧的原长0A=0.3m;然后小球由静止释放,小球到达距O点下方h=0.5m处的B点时速度为VB=2m/s,求
如图所示,质量为m=2kg的小球系在轻质弹簧的一端,另一端固定在悬点O处,将弹簧拉至水平位置A处,且弹簧处于自然状态,弹簧的原长0A=0.3m;然后小球由静止释放,小球到达距O点下方h=0.5m处的B点时速度为VB=2m/s,求 处于静止状态.两车之间有一感应机关,在它的作用下,当滑块滑过两车连接处时,两车将自动分离.现剪断细线,滑块先后在甲、乙小车上滑行,最终滑块恰好滑到乙车的另一端而未滑出乙车.取g=10m/s2,求:
处于静止状态.两车之间有一感应机关,在它的作用下,当滑块滑过两车连接处时,两车将自动分离.现剪断细线,滑块先后在甲、乙小车上滑行,最终滑块恰好滑到乙车的另一端而未滑出乙车.取g=10m/s2,求: 如图所示,一辆质量为M=6kg的小车静止在光滑的水平面上,另一质量为m=2kg的物块(可视为质点)静止在小车上的A点;在物块和小车右侧的挡板之间夹有一被压缩的轻质弹簧(弹簧和物块不相连),弹簧的弹性势能为4J,物块和挡板之间用细线连结.已知物块和小车之间的动摩擦因数μ=0.2.某时刻将细线烧断,弹簧将物块弹开,最后物块停在小车上的B点,取g=10m/s2.
如图所示,一辆质量为M=6kg的小车静止在光滑的水平面上,另一质量为m=2kg的物块(可视为质点)静止在小车上的A点;在物块和小车右侧的挡板之间夹有一被压缩的轻质弹簧(弹簧和物块不相连),弹簧的弹性势能为4J,物块和挡板之间用细线连结.已知物块和小车之间的动摩擦因数μ=0.2.某时刻将细线烧断,弹簧将物块弹开,最后物块停在小车上的B点,取g=10m/s2.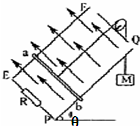 如图所示,无限长金属导轨EF、PQ固定在倾角为θ=30°的光滑绝缘斜面上,轨道间距L=1m,底部接入一阻值为R=0.4Ω的定值电阻,上端开口.垂直斜面向上的匀强磁场的磁感应强度B=2T.一质量为m=0.8kg的金属棒ab与导轨接触良好,ab与导轨间没有摩擦,ab连入导轨间的电阻r=0.1Ω,电路中其余电阻不计.现用一质量为M=2kg的物体通过一不可伸长的轻质细绳绕过光滑的定滑轮与ab相连.由静止释放M,不计空气阻力,当M下落高度h=2.0m时,ab开始匀速运动(运动中ab始终垂直导轨,并接触良好,g=10m/s2).求:
如图所示,无限长金属导轨EF、PQ固定在倾角为θ=30°的光滑绝缘斜面上,轨道间距L=1m,底部接入一阻值为R=0.4Ω的定值电阻,上端开口.垂直斜面向上的匀强磁场的磁感应强度B=2T.一质量为m=0.8kg的金属棒ab与导轨接触良好,ab与导轨间没有摩擦,ab连入导轨间的电阻r=0.1Ω,电路中其余电阻不计.现用一质量为M=2kg的物体通过一不可伸长的轻质细绳绕过光滑的定滑轮与ab相连.由静止释放M,不计空气阻力,当M下落高度h=2.0m时,ab开始匀速运动(运动中ab始终垂直导轨,并接触良好,g=10m/s2).求: