Question

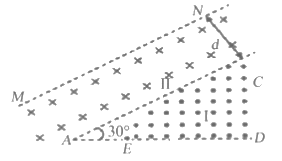
【题目】如图所示，在Ⅰ、Ⅱ两个区域内存在磁感应强度大小均为B的匀强磁场，磁场方向分别垂直于纸面向外和向里，AD、AC边界的夹角∠DAC＝30°，边界AC与边界MN平行，Ⅱ区域宽度为d，长度无限大。质量为m、电荷量为+q的粒子可在边界AD上的不同点射入，入射速度垂直于AD且垂直于磁场，若入射速度大小为，不计粒子重力，Ⅰ区磁场右边界距A点无限远。求：

（1）从距A点d处的E射入的粒子在磁场区域内运动的时间；

（2）粒子在磁场区域内运动的最短时间；

（3）从MN边界出射粒子的区域长度。

Answer 1

【答案】（1）（2）（3）

【解析】

(1)粒子做匀速圆周运动，根据向心力公式，有

其中：

解得r=d；画出粒子恰好不进入II区的临界轨迹，如图所示：

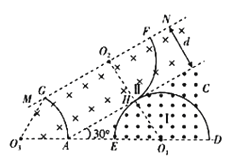
结合几何关系，有：

粒子从E点射入后，在I区域做圆周，然后进入II区域，做圆周运动有：

故运动时间为：

(2)从A点进入的粒子在磁场中运动的轨迹最短（弦长也最短），时间最短轨迹如图所示，由几何关系可知轨迹对应的圆心角为60°，故最短时间为：

(3)刚好从A点射入II区域的粒子射到MN上时位于最下端，即图中的G点；刚好进入II区域的粒子射到MN上时位于最上端，此时粒子沿AC方向从H点射入II区域，转一个圆弧从MN上F点射出，根据几何关系可知GF间的距离：

答：（1）从距A点d处的E射入的粒子在磁场区域内运动的时间；

（2）粒子在磁场区域内运动的最短时间；

（3）从MN边界出射粒子的区域长度。