题目内容
17.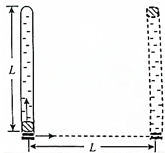 如图所示,一端封闭的玻璃管中注满清水,水中放一个用红蜡做成的小圆柱体(小圆柱体可看作质点且恰能在管中匀速上浮),将玻璃管的开口端用胶塞塞紧,然后将玻璃管迅速竖直倒置,在红蜡块匀速上浮的同时使玻璃管从静止开始水平向右匀加速移动,当玻璃管向右水平运动的距离等于管长时,红蜡块在竖直方向刚好到达管顶,若测得玻璃管长为L,此过程用时为t,那么红蜡块在此过程中相对于地( )
如图所示,一端封闭的玻璃管中注满清水,水中放一个用红蜡做成的小圆柱体(小圆柱体可看作质点且恰能在管中匀速上浮),将玻璃管的开口端用胶塞塞紧,然后将玻璃管迅速竖直倒置,在红蜡块匀速上浮的同时使玻璃管从静止开始水平向右匀加速移动,当玻璃管向右水平运动的距离等于管长时,红蜡块在竖直方向刚好到达管顶,若测得玻璃管长为L,此过程用时为t,那么红蜡块在此过程中相对于地( )| A. | 做匀变速直线运动 | |
| B. | 加速度大小为$\frac{L}{{t}^{2}}$ | |
| C. | 运动到玻璃管中点时的速度大小为$\frac{\sqrt{2}L}{t}$ | |
| D. | 运动到玻璃管中点时的速度大小为$\frac{\sqrt{3}L}{t}$ |
分析 蜡块参加了两个分运动:水平向右的匀加速直线运动和竖直向上的匀速直线运动,根据分位移公式求加速度.将分运动的速度合成可以得到合运动速度大小.
解答 解:A、蜡块在水平方向上做水平向右的匀加速直线运动,竖直方向向上做匀速直线运动,合运动是匀变速曲线运动,故A错误.
B、根据水平方向的分运动得:L=$\frac{1}{2}a{t}^{2}$;得 a=$\frac{2L}{{t}^{2}}$,故B错误.
CD、竖直方向上有 L=vyt,得vy=$\frac{L}{t}$.运动到玻璃管中点时的时间为 t′=$\frac{\frac{L}{2}}{{v}_{y}}$=$\frac{t}{2}$,水平分速度 vx=at′=$\frac{L}{t}$
故速度大小为为 v=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$=$\frac{\sqrt{2}L}{t}$,故C正确,D错误.
故选:C
点评 本题的关键要熟练运用分解法研究类平抛运动,由分运动的位移规律和速度规律进行解答,分析时还要抓住分运动的同时性.

练习册系列答案
相关题目
8.下面关于带电粒子在电场中和磁场中受力情况的说法中正确的是( )
| A. | 静止的带电粒子在电场中要受电场力作用,但运动的带电粒子在电场中不受电场力作用 | |
| B. | 静止的带电粒子在磁场中不受磁场力作用,但运动的带电粒子在磁场中必定要受磁场力作用 | |
| C. | 带电粒子在电场中受到的电场力方向一定与电场方向相同 | |
| D. | 若运动的带电粒子在磁场中受到磁场力的作用,那么磁场力的方向必定与磁场方向垂直,也与粒子的运动方向垂直 |
5.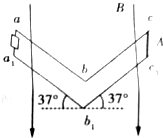 如图所示,电阻不计的两平行光滑导轨abc和a1b1c1竖直放置,两导轨长度都为2L,间距为d,且从中点b、b1处平滑变曲成“V”形,导轨两侧与水平面间的夹角均为37°,两导轨左端a、a1间连接一阻值为R的定值电阻.在导轨所在空间有竖直向下的匀强磁场,磁感应强度大小为B.现在导轨右端cc1处由静止释放一质量为m、长度为d、电阻为R的导体棒A,导体棒A垂直两导轨且始终与两导轨接触良好,当导体棒A运动至bc中间位置时开始沿导轨向下做匀速运动.已知重力加速度大小为g,sin37°=0.6,cos37°=0.8,则下列说法正确的是(提示:当B与c不垂直时,可以将B分解)( )
如图所示,电阻不计的两平行光滑导轨abc和a1b1c1竖直放置,两导轨长度都为2L,间距为d,且从中点b、b1处平滑变曲成“V”形,导轨两侧与水平面间的夹角均为37°,两导轨左端a、a1间连接一阻值为R的定值电阻.在导轨所在空间有竖直向下的匀强磁场,磁感应强度大小为B.现在导轨右端cc1处由静止释放一质量为m、长度为d、电阻为R的导体棒A,导体棒A垂直两导轨且始终与两导轨接触良好,当导体棒A运动至bc中间位置时开始沿导轨向下做匀速运动.已知重力加速度大小为g,sin37°=0.6,cos37°=0.8,则下列说法正确的是(提示:当B与c不垂直时,可以将B分解)( )
 如图所示,电阻不计的两平行光滑导轨abc和a1b1c1竖直放置,两导轨长度都为2L,间距为d,且从中点b、b1处平滑变曲成“V”形,导轨两侧与水平面间的夹角均为37°,两导轨左端a、a1间连接一阻值为R的定值电阻.在导轨所在空间有竖直向下的匀强磁场,磁感应强度大小为B.现在导轨右端cc1处由静止释放一质量为m、长度为d、电阻为R的导体棒A,导体棒A垂直两导轨且始终与两导轨接触良好,当导体棒A运动至bc中间位置时开始沿导轨向下做匀速运动.已知重力加速度大小为g,sin37°=0.6,cos37°=0.8,则下列说法正确的是(提示:当B与c不垂直时,可以将B分解)( )
如图所示,电阻不计的两平行光滑导轨abc和a1b1c1竖直放置,两导轨长度都为2L,间距为d,且从中点b、b1处平滑变曲成“V”形,导轨两侧与水平面间的夹角均为37°,两导轨左端a、a1间连接一阻值为R的定值电阻.在导轨所在空间有竖直向下的匀强磁场,磁感应强度大小为B.现在导轨右端cc1处由静止释放一质量为m、长度为d、电阻为R的导体棒A,导体棒A垂直两导轨且始终与两导轨接触良好,当导体棒A运动至bc中间位置时开始沿导轨向下做匀速运动.已知重力加速度大小为g,sin37°=0.6,cos37°=0.8,则下列说法正确的是(提示:当B与c不垂直时,可以将B分解)( )| A. | 导体棒A能到达导轨的左端aa1处 | |
| B. | 导体棒A沿右侧导轨向下做匀速运动时的速率为$\frac{15mgR}{8{B}^{2}{d}^{2}}$ | |
| C. | 最终通过定值电阻的电荷量为零 | |
| D. | 最终定值电阻中产生的热量为$\frac{3}{10}$mgL |
2.从同一高度以不同的速度水平抛出的两个物体落到地面的时间( )
| A. | 速度大的时间长 | |
| B. | 速度小的时间长 | |
| C. | 物体落地时的水平位移与初速度有关 | |
| D. | 物体落地时的水平位移与抛出点的高度无关 |

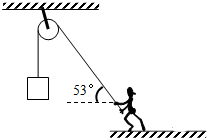 如图所示,重力为500N的人通过定滑轮的轻绳牵引重为200N的物体,当绳与水平面成角时,物体和人都静止,不计滑轮与绳间的摩擦力,求人对地面的压力和摩擦力.(sin53°=0.8 cos53°=0.6)
如图所示,重力为500N的人通过定滑轮的轻绳牵引重为200N的物体,当绳与水平面成角时,物体和人都静止,不计滑轮与绳间的摩擦力,求人对地面的压力和摩擦力.(sin53°=0.8 cos53°=0.6)