题目内容
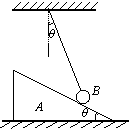 质量为M的斜面体A放在粗糙水平面上,用轻绳拴住质量为m的小球B置于斜面上,整个系统处于静止状态,已知斜面倾角及轻绳与竖直方向夹角均为 θ=30°.不计小球与斜面间的摩擦,求:
质量为M的斜面体A放在粗糙水平面上,用轻绳拴住质量为m的小球B置于斜面上,整个系统处于静止状态,已知斜面倾角及轻绳与竖直方向夹角均为 θ=30°.不计小球与斜面间的摩擦,求:(1)斜面对小球的作用力大小
(2)斜面体对水平面的压力大小
(3)斜面体与水平面间的摩擦力大小.
分析:(1)对小球进行受力分析,根据共点力平衡求出斜面对小球的作用力.
(2、3)对斜面体进行受力分析,根据正交分解求出地面的支持力和摩擦力.
(2、3)对斜面体进行受力分析,根据正交分解求出地面的支持力和摩擦力.
解答:解:(1)小球的受力分析如图.
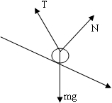 拉力和支持力与竖直方向上的夹角都为30°,根据正交分解得:
拉力和支持力与竖直方向上的夹角都为30°,根据正交分解得:
Tsin30°=Nsin30°
Tcos30°+Ncos30°=mg
联立两式解得:N=
mg.
答:斜面对小球的作用力大小为
mg.
(2、3)对斜面体进行受力分析,如图.
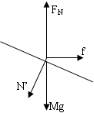 根据正交分解得:
根据正交分解得:
竖直方向上:FN=N′cos30°+Mg=
mg+Mg
由牛顿第三定律得斜面体对水平面的压力大小为FN'=
mg+Mg
水平方向上:f=N′sin30°=
mg
则斜面体与水平面间的摩擦力大小为
mg.
答:斜面体对水平面的压力大小为
mg+Mg,斜面体与水平面间的摩擦力大小为
mg.
 拉力和支持力与竖直方向上的夹角都为30°,根据正交分解得:
拉力和支持力与竖直方向上的夹角都为30°,根据正交分解得:Tsin30°=Nsin30°
Tcos30°+Ncos30°=mg
联立两式解得:N=
| ||
| 3 |
答:斜面对小球的作用力大小为
| ||
| 3 |
(2、3)对斜面体进行受力分析,如图.
 根据正交分解得:
根据正交分解得:竖直方向上:FN=N′cos30°+Mg=
| 1 |
| 2 |
由牛顿第三定律得斜面体对水平面的压力大小为FN'=
| 1 |
| 2 |
水平方向上:f=N′sin30°=
| ||
| 6 |
则斜面体与水平面间的摩擦力大小为
| ||
| 6 |
答:斜面体对水平面的压力大小为
| 1 |
| 2 |
| ||
| 6 |
点评:解决本题的关键是正确的选取研究对象,进行受力分析,运用正交分解进行求解.解答中要注意应用牛顿第三定律.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 如图所示,在粗糙水平地面上,放一个质量为M的斜面体b,若一质量为m的物体a在斜面上匀速下滑,则( )
如图所示,在粗糙水平地面上,放一个质量为M的斜面体b,若一质量为m的物体a在斜面上匀速下滑,则( )