��Ŀ����
����Ŀ��������Ϊm=75kg�Ļ�ѩ���Գ��ٶ�v0=8m/s�������Ϊ��=37���б���������ɻ��У���֪ѩ����б���Ķ�Ħ��������=0.25������б���㹻��sin 37��=0.6��gȡ10m/s2 �� ���ƿ�������������
��1��������ѩ�ߵ���������ͼ��
��2����ѩ����б���ϻ��������룻
��3������ѩ��������ߵ���ת�����������ɻ��У������������ʱ���ٶȴ�С��
���𰸡�
��1���⣺��ѩ����б���������ɻ���ʱ���ܵ���ֱ���µ���������б�����µ�Ħ�����ʹ�ֱ��б�����ϵ�֧��������ͼ��ʾ��
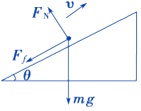
��2���⣺��ţ�ٵڶ����ɵã�
mgsin37��+Ff=ma1����
����ΪFf=��FN����
FN=mgcos37�㡭��
�����٢ڢ۴������ݿɽ�ã�a1=8m/s2��
��ѩ����б���������ȼ���ֱ���˶����ٶȼ�С����ʱ��λ��Ϊ��
x= ![]() =
= ![]() m=4m��
m=4m��
��Ϊ��ѩ����б���ϻ���������
�𣺻�ѩ����б���ϻ���������Ϊ4m
��3���⣺����ѩ����б���������ɻ���ʱ���ܵ���ֱ���µ���������б�����ϵ�Ħ�����ʹ�ֱ��б�����ϵ�֧��������ͼ��ʾ��
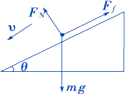
��ţ�ٵڶ����ɵã�
mgsin37�㩁Ff=ma2����
����ΪFf=��FN����
FN=mgcos37�㡭��
�����ܢݢ������ݿɽ�ã�a2=4m/s2��
��ѩ����б�����������ٶ�Ϊ����ȼ���ֱ���˶�������������ʱ��λ�ƴ�Сx=4m��
��v2=2ax�ã���ѩ�������ʱ���ٶȴ�С��
v= ![]() =
= ![]() m/s=4
m/s=4 ![]() m/s
m/s
�����������ʱ���ٶȴ�СΪ4 ![]() m/s
m/s
����������1����ѩ����б���������ɻ���ʱ���Ի�ѩ�������������ɵ�����ʾ��ͼ����2������ţ�ٵڶ����ɿ��������ѩ����б�����ϻ���ʱ�ļ��ٶȣ�Ӧ���ȱ���ֱ���˶����ٶ�λ�ƹ�ʽ������ϻ��еľ��룻��3������ţ�ٵڶ����ɿ��������ѩ����б�����»���ʱ�ļ��ٶȣ�Ӧ���ȱ���ֱ���˶����ٶ�λ�ƹ�ʽ������������ʱ���ٶȴ�С��
�����㾫����������Ҫ�����˻���Ħ�������ȱ���ֱ���˶����ٶȡ�λ�ơ�ʱ��Ĺ�ϵ�����֪ʶ�㣬��Ҫ���ջ���Ħ����:���ù�ʽf=��F N ���м��㣬����FN ���������ѹ������һ������������������������ܺ�������.���߸���������˶�״̬������ƽ��������ţ�ٶ�������⣻�ٶȹ�ʽ��V=V0+at��λ�ƹ�ʽ��s=v0t+1/2at2���ٶ�λ�ƹ�ʽ��vt2-v02=2as�����ϸ�ʽ��Ϊʸ��ʽ��Ӧ��ʱӦ�涨������Ȼ���ʸ����Ϊ��������⣬ͨ��ѡ���ٶȷ���Ϊ�������Ǹ�������һ�µ�ȡ��+��ֵ�����������෴��ȡ��-��ֵ������ȷ�����⣮

 A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д� ȫ�Ų��Ծ�ϵ�д�
ȫ�Ų��Ծ�ϵ�д�