题目内容
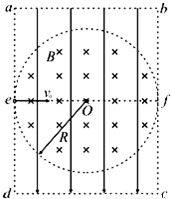
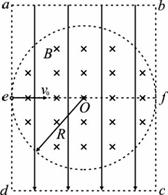
 如图所示,真空中的矩形abcd区域内存在竖直向下的匀强电场,半径为R的圆形区域内同时存在垂直于纸面向里的匀强磁场,磁感应强度为B,圆形边界分别相切于ad、bc边的中点e、f.一带电粒子以初速度v0沿着ef方向射入该区域后能做直线运动;当撤去磁场并保留电场,粒子以相同的初速度沿着ef方向射入恰能从c点飞离该区域.已知ad=bc=
如图所示,真空中的矩形abcd区域内存在竖直向下的匀强电场,半径为R的圆形区域内同时存在垂直于纸面向里的匀强磁场,磁感应强度为B,圆形边界分别相切于ad、bc边的中点e、f.一带电粒子以初速度v0沿着ef方向射入该区域后能做直线运动;当撤去磁场并保留电场,粒子以相同的初速度沿着ef方向射入恰能从c点飞离该区域.已知ad=bc=4
| ||
| 3 |
(1)带电粒子的电荷量q与质量m的比值
| q |
| m |
(2)若撤去电场保留磁场,粒子离开矩形区域时的位置.
分析:(1)本题先分析带电粒子的运动情况,并把握每个过程遵守的规律:未撤去磁场时,带电粒子做匀速直线运动,电场力与洛伦兹力平衡;撤去磁场后,带电粒子做类平抛运动,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,已知水平距离x=2R,竖直距离y=
bc=
R,根据牛顿第二定律和运动学公式结合求出比荷.
(2)若撤去电场保留磁场,粒子将在洛伦兹力作用下做匀速圆周运动,由牛顿第二定律可求得轨迹半径,画出轨迹,由几何关系求出粒子离开矩形区域时的位置.
| 1 |
| 2 |
2
| ||
| 3 |
(2)若撤去电场保留磁场,粒子将在洛伦兹力作用下做匀速圆周运动,由牛顿第二定律可求得轨迹半径,画出轨迹,由几何关系求出粒子离开矩形区域时的位置.
解答: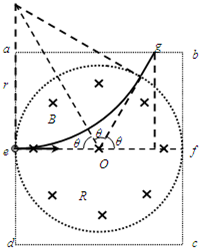 解:(1)设匀强电场强度为E,当电场和磁场同时存在时,粒子沿ef方向做直线运动,有:
解:(1)设匀强电场强度为E,当电场和磁场同时存在时,粒子沿ef方向做直线运动,有:
qv0B=qE…①
当撤去磁场,保留电场时,带电粒子做类平抛运动,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,由题,粒子恰能从c点飞出,则
水平方向有:2R=v0t ②
竖直方向有:
bc=
at2 ③
qE=ma ④
联解①②③④得:
=
…⑤
(2)若撤去电场保留磁场,粒子将在洛伦兹力作用下做匀速圆周运动,轨迹如图所示.
设粒子离开矩形区域时的位置g离b的距离为x,则由牛顿第二定律:
qv0B=m
…⑦
得,r=
=
?
=
R
由图中几何关系得:
粒子的轨迹半径为r=Rtanθ=
R…⑧
得θ=60°
故粒子离开磁场时到b的距离为x=
ab-
bc?cotθ…⑨
代入解得:x=
…⑩
答:
(1)带电粒子的电荷量q与质量m的比值
等于
.
(2)若撤去电场保留磁场,粒子离开矩形区域时的位置离b的距离为
.
 解:(1)设匀强电场强度为E,当电场和磁场同时存在时,粒子沿ef方向做直线运动,有:
解:(1)设匀强电场强度为E,当电场和磁场同时存在时,粒子沿ef方向做直线运动,有:qv0B=qE…①
当撤去磁场,保留电场时,带电粒子做类平抛运动,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,由题,粒子恰能从c点飞出,则
水平方向有:2R=v0t ②
竖直方向有:
| 1 |
| 2 |
| 1 |
| 2 |
qE=ma ④
联解①②③④得:
| q |
| m |
| ||
| 3BR |
(2)若撤去电场保留磁场,粒子将在洛伦兹力作用下做匀速圆周运动,轨迹如图所示.
设粒子离开矩形区域时的位置g离b的距离为x,则由牛顿第二定律:
qv0B=m
| v2 |
| r |
得,r=
| mv0 |
| qB |
| 3BR | ||
|
| v0 |
| B |
| 3 |
由图中几何关系得:
粒子的轨迹半径为r=Rtanθ=
| 3 |
得θ=60°
故粒子离开磁场时到b的距离为x=
| 1 |
| 2 |
| 1 |
| 2 |
代入解得:x=
| R |
| 3 |
答:
(1)带电粒子的电荷量q与质量m的比值
| q |
| m |
| ||
| 3BR |
(2)若撤去电场保留磁场,粒子离开矩形区域时的位置离b的距离为
| R |
| 3 |
点评:本题中带电粒子在复合场中运动,分析受力情况和运动情况是基础,磁场中关键画出轨迹,运用几何知识求解轨迹半径.

练习册系列答案
相关题目
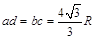 ,忽略粒子的重力。求:
,忽略粒子的重力。求: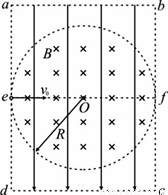
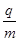 ;
; ,忽略粒子的重力。求:
,忽略粒子的重力。求: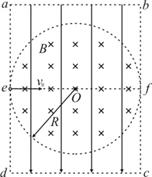
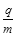 ;
;
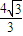 R,忽略粒子的重力.求:
R,忽略粒子的重力.求: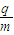 ;
;