题目内容
16.在同一匀强磁场中,α粒子(${\;}_{2}^{4}$He)和质子(${\;}_{1}^{1}$H)做匀速圆周运动,若它们的动量大小相等,则α粒子和质子( )| A. | 运动半径之比是2:1 | B. | 运动周期之比是2:1 | ||
| C. | 运动速度大小之比是4:1 | D. | 受到的洛伦兹力之比是2:1 |
分析 质子H和α粒子以相同的动量在同一匀强磁场中作匀速圆周运动,均由洛仑兹力提供向心力,由牛顿第二定律和圆周运动的规律,可求得比较r、速度v及T的表达式,根据表达式可以得到半径以及周期之比.
解答 解:C、两个粒子的动量大小相等,质量之比是4:1,
所以:$\frac{{v}_{He}}{{v}_{H}}=\frac{{m}_{H}}{{m}_{He}}=\frac{1}{4}$.故C错误;
A、质子H和α粒子在匀强磁场中作匀速圆周运动,均由洛仑兹力提供向心力,由牛顿第二定律得:
qvB=m$\frac{{v}^{2}}{R}$,得轨道半径:R=$\frac{mv}{qB}$=$\frac{P}{qB}$,
根据质子质子(${\;}_{1}^{1}$H)和α(${\;}_{2}^{4}$He)粒子的电荷量之比是1:2,质量之比是1:4,
则得:RHe:RH=$\frac{{q}_{H}}{{q}_{He}}=\frac{1}{2}$,故A错误;
B、粒子运动的周期:$T=\frac{2πr}{v}$,所以:$\frac{{T}_{He}}{{T}_{H}}=\frac{\frac{{R}_{He}}{{v}_{He}}}{\frac{{R}_{H}}{{v}_{H}}}=\frac{{R}_{He}}{{R}_{H}}•\frac{{v}_{H}}{{v}_{He}}=\frac{1}{2}×\frac{4}{1}=\frac{2}{1}$.故B正确;
D、根据粒子受到的洛伦兹力:f=qvB,得:$\frac{{f}_{He}}{{f}_{H}}=\frac{{q}_{He}•{v}_{He}}{{q}_{H}•{v}_{H}}=\frac{2}{1}×\frac{1}{4}=\frac{1}{2}$.故D错误.
故选:B
点评 本题主要考查了带电粒子在磁场场中运动的问题,知道洛伦兹力充当向心力,熟练掌握圆周运动的基本公式即可.

 在如图所示的电路中,电源电动势为E,内阻为r,电流表A、二极管和电压表V1、V2均为理想元件,R1为定值电阻,R2为滑动变阻器.闭合开关S,当R2的滑动触头P向下滑动的过程中( )
在如图所示的电路中,电源电动势为E,内阻为r,电流表A、二极管和电压表V1、V2均为理想元件,R1为定值电阻,R2为滑动变阻器.闭合开关S,当R2的滑动触头P向下滑动的过程中( )| A. | 电压表V1的示数增大,电压表V2的示数减小 | |
| B. | 电压表V1示数变化量的绝对值与电压表V2示数变化量的绝对值相等 | |
| C. | 电容器上的电压与电流表A示数的比值不变 | |
| D. | 电压表V1示数的变化量与电流表A示数的变化量的比值保持不变 |
| A. | 地震时释放的巨大能量引发海啸,能将震源附近的海水推到几千千米远的地方 | |
| B. | 载人飞船设计时需设法减少发射过程中与航天员身体固有频率相近的超低频振动 | |
| C. | 无线网络信号能绕过障碍物传递到接收终端是利用了干涉原理 | |
| D. | 立体放映机双镜头中的一个镜头发生故障时,观众戴着偏振光眼镜也能体验立体效果 |
| A. | 10m/s | B. | 5m/s | C. | 7m/s | D. | 15m/s |
 某科研单位设计了一空间飞行器,飞行器从地面起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰恰与水平方向成θ=30°角的直线斜向右上方由静止开始匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是( )
某科研单位设计了一空间飞行器,飞行器从地面起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰恰与水平方向成θ=30°角的直线斜向右上方由静止开始匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是( )| A. | 加速时动力的大小等于mg | |
| B. | 加速与减速时的加速度大小之比为2:$\sqrt{3}$ | |
| C. | 加速与减速过程发生的位移大小之比为1:2 | |
| D. | 减速飞行时间2t后速度为零 |
 如图,竖直平面内的$\frac{3}{4}$圆弧形光滑轨道半径为R,C端与圆心O等高,D端在O的正上方,BE为与水平方向成θ角的光滑斜面,B点在C端的正上方.一个可看成质点的小球从距地面H=$\frac{8}{3}$R处的A点由静止开始释放,自由下落至C点后进入圆弧形轨道,过D点后恰好从斜面BE的B点滑上斜面(无碰撞现象).
如图,竖直平面内的$\frac{3}{4}$圆弧形光滑轨道半径为R,C端与圆心O等高,D端在O的正上方,BE为与水平方向成θ角的光滑斜面,B点在C端的正上方.一个可看成质点的小球从距地面H=$\frac{8}{3}$R处的A点由静止开始释放,自由下落至C点后进入圆弧形轨道,过D点后恰好从斜面BE的B点滑上斜面(无碰撞现象).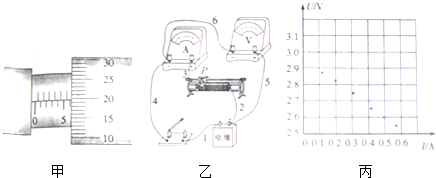
 一半径为R的半圆柱形玻璃砖,横截面如图所示.已知玻璃的全反射临界角为γ(γ<$\frac{π}{3}$).与玻璃砖的底平面成($\frac{π}{2}$-γ)角度、且与玻璃砖横截面平行的平行光射到玻璃砖的半圆柱面上.经柱面折射后,有部分光(包括与柱面相切的入射光)能直接从玻璃砖底面射出,若忽略经半圆柱内表面反射后射出的光,求底面透光部分的宽度.
一半径为R的半圆柱形玻璃砖,横截面如图所示.已知玻璃的全反射临界角为γ(γ<$\frac{π}{3}$).与玻璃砖的底平面成($\frac{π}{2}$-γ)角度、且与玻璃砖横截面平行的平行光射到玻璃砖的半圆柱面上.经柱面折射后,有部分光(包括与柱面相切的入射光)能直接从玻璃砖底面射出,若忽略经半圆柱内表面反射后射出的光,求底面透光部分的宽度. 如图,轨道ABCD固定在竖直平面内,ABC段光滑,BC段是以O(A与O在同一直线上)为圆心,半径R=10m的圆弧管道,水平平台CD与圆弧管道下端C点相切,质量m=4kg的物块(可视为质点)以水平初速度v0=15m/s从A开始始终沿轨道运动,最后停留在D点,物块与CD间的动摩擦因数μ=0.25,取g=10m/s2,求:
如图,轨道ABCD固定在竖直平面内,ABC段光滑,BC段是以O(A与O在同一直线上)为圆心,半径R=10m的圆弧管道,水平平台CD与圆弧管道下端C点相切,质量m=4kg的物块(可视为质点)以水平初速度v0=15m/s从A开始始终沿轨道运动,最后停留在D点,物块与CD间的动摩擦因数μ=0.25,取g=10m/s2,求: