题目内容
4.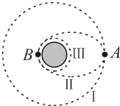 我国月球探测活动的第一步“绕月”工程和第二步“落月”工程已按计划在2013年以前顺利完成.假设月球半径为R,月球表面的重力加速度为g0,飞船沿距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B时再次点火进入月球近月轨道Ⅲ绕月球做圆周运动,下列判断正确的是( )
我国月球探测活动的第一步“绕月”工程和第二步“落月”工程已按计划在2013年以前顺利完成.假设月球半径为R,月球表面的重力加速度为g0,飞船沿距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B时再次点火进入月球近月轨道Ⅲ绕月球做圆周运动,下列判断正确的是( )| A. | 飞船从A到B运行的过程中机械能增大 | |
| B. | 飞船在A点处点火变轨时,动能增大 | |
| C. | 飞船在轨道Ⅰ上的运行速率v=$\frac{\sqrt{{g}_{0}R}}{2}$ | |
| D. | 飞船在轨道Ⅲ绕月球运动一周所需的时间T=π$\sqrt{\frac{R}{{g}_{0}}}$ |
分析 根据机械能守恒条件判断A到B过程中机械能守恒,结合万有引力与向心力的大小关系,判断在A点是加速还是减速.根据万有引力提供向心力和万有引力等于重力求出飞船在轨道Ⅰ和轨道Ⅲ上的运行速率和周期.
解答 解:A、飞船从A到B的过程中只有万有引力做功,机械能守恒,故A错误.
B、飞船在A点从轨道Ⅰ进入轨道Ⅱ,需减速,使得万有引力大于向心力,做近心运动,所以动能减小,故B错误.
C、根据$G\frac{Mm}{(4R)^{2}}=m\frac{{v}^{2}}{4R}$得,飞船的运行速率v=$\sqrt{\frac{GM}{4R}}$,又GM=${g}_{0}{R}^{2}$,则v=$\frac{\sqrt{{g}_{0}R}}{2}$.故C正确.
D、根据$G\frac{Mm}{{R}^{2}}=mR\frac{4{π}^{2}}{{T}^{2}}$得,飞船在轨道Ⅲ上的周期T=$\sqrt{\frac{4{π}^{2}{R}^{3}}{GM}}$,又GM=${g}_{0}{R}^{2}$,解得T=$2π\sqrt{\frac{R}{{g}_{0}}}$,故D错误.
故选:C.
点评 解决本题的关键掌握变轨的原理,以及掌握万有引力定律的两个重要理论:1、万有引力等于重力,2、万有引力提供向心力,并能灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列说法中正确的是( )
| A. | 军队士兵过桥时使用便步,是为了防止桥发生共振现象 | |
| B. | 机械波和电磁波在介质中的传播速度仅由介质决定 | |
| C. | 泊松亮斑是光通过圆孔发生衍射时形成的 | |
| D. | 拍摄玻璃橱窗内的物品时,在镜头前加装一个偏振片以减弱玻璃的反射光 |
9.下列说法正确的是( )
| A. | 自然界中进行的一切与热现象有关的宏观过程都具是可逆的 | |
| B. | 若气体的温度逐渐升高,其压强可以保持不变 | |
| C. | 温度相同的氢气和氧气,氢气分子和氧气分子的平均速率相同 | |
| D. | 只要知道气体的摩尔体积和阿伏加德罗常数,就可以算出气体分子的体积 |
16.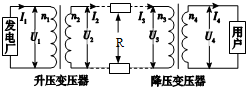 远距离输电的原理图如图所示,升降压变压器原副线圈的匝数、电压、电流、线路电阻如图.变压器为理想变压器,则下列关系式正确的是( )
远距离输电的原理图如图所示,升降压变压器原副线圈的匝数、电压、电流、线路电阻如图.变压器为理想变压器,则下列关系式正确的是( )
 远距离输电的原理图如图所示,升降压变压器原副线圈的匝数、电压、电流、线路电阻如图.变压器为理想变压器,则下列关系式正确的是( )
远距离输电的原理图如图所示,升降压变压器原副线圈的匝数、电压、电流、线路电阻如图.变压器为理想变压器,则下列关系式正确的是( )| A. | $\frac{{I}_{1}}{{I}_{2}}$=$\frac{{n}_{1}}{{n}_{2}}$ | B. | I2=$\frac{{U}^{2}}{R}$ | ||
| C. | I1U1=I2U2 | D. | 若n2增加,用户得到的电压增大 |
13.下列有关物理学史的说法中正确的是( )
| A. | 赫兹最早发现了电磁感应现象 | |
| B. | 奥斯特发现了电流的磁效应,并总结出了右手螺旋定则 | |
| C. | 安培通过实验发现了在磁场中产生电流的条件 | |
| D. | 库仑发现了电荷之间的相互作用规律--库仑定律 |
 如图所示,某工厂要把货物(可视为质点)由斜面的顶端运送到底端,为保证货物的安全,斜面上光滑区域与粗糙区域(粗糙程度相同)交替出现,各区域宽度均相等,已知斜面长为L,倾角为θ.货物从斜面顶端A点由静止释放,到达斜面底端B点时速度恰好为零,整个过程运动时间为t.求:
如图所示,某工厂要把货物(可视为质点)由斜面的顶端运送到底端,为保证货物的安全,斜面上光滑区域与粗糙区域(粗糙程度相同)交替出现,各区域宽度均相等,已知斜面长为L,倾角为θ.货物从斜面顶端A点由静止释放,到达斜面底端B点时速度恰好为零,整个过程运动时间为t.求: