题目内容
 一根长度为L的轻质直杆两端各固定一个可视为质点的小球A和B,两小球质量均为m,直杆可以绕过其中点O的水平轴在竖直平面内匀速转动,若直杆匀速转动周期为2π
一根长度为L的轻质直杆两端各固定一个可视为质点的小球A和B,两小球质量均为m,直杆可以绕过其中点O的水平轴在竖直平面内匀速转动,若直杆匀速转动周期为2π
|
(1)小球转动的角速度;
(2)直杆转动到如图竖直位置时,A、B两小球对直杆作用力各多大?方向如何?
分析:(1)根据ω=
求出小球转动的角速度.
(2)对两个小球受力分析,在竖直方向的合力提供圆周运动的向心力,根据牛顿第二定律求出杆子的作用力大小和方向.
| 2π |
| T |
(2)对两个小球受力分析,在竖直方向的合力提供圆周运动的向心力,根据牛顿第二定律求出杆子的作用力大小和方向.
解答:解:(1)已知小球的转动周期T=2π
,
故小球转动的角速度ω=
=
…①
(2)以A小球为研究对象,在最高点的受力如图,设NA方向向上,
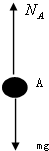
根据牛顿第二定律得:mg-NA=mω2
…②
由①②式得:NA=
mg…③
根据牛顿第三定律得,A球对直杆有竖直向下的压力,
大小为NA′=NA=
mg…④
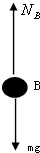
以B小球为研究对象,在最低点的受力如图,设NB方向向上,根据牛顿第二定律得:NB-mg=mω2
…⑤
由①⑤式得:NB=
mg…⑥
根据牛顿第三定律得,B球对直杆有竖直向下的拉力,
大小为NB′=NB=
mg…⑦
故A球对直杆有竖直向下的压力,大小为
mg.B球对直杆有竖直向下的拉力,大小为
mg.
|
故小球转动的角速度ω=
| 2π |
| T |
|
(2)以A小球为研究对象,在最高点的受力如图,设NA方向向上,

根据牛顿第二定律得:mg-NA=mω2
| L |
| 2 |
由①②式得:NA=
| 1 |
| 2 |
根据牛顿第三定律得,A球对直杆有竖直向下的压力,
大小为NA′=NA=
| 1 |
| 2 |

以B小球为研究对象,在最低点的受力如图,设NB方向向上,根据牛顿第二定律得:NB-mg=mω2
| L |
| 2 |
由①⑤式得:NB=
| 3 |
| 2 |
根据牛顿第三定律得,B球对直杆有竖直向下的拉力,
大小为NB′=NB=
| 3 |
| 2 |
故A球对直杆有竖直向下的压力,大小为
| 1 |
| 2 |
| 3 |
| 2 |
点评:解决本题要知道,小球沿半径方向的合力提供做圆周运动的向心力,注意杆子和绳子不同,绳子只能表现为拉力,杆子既可以表现为拉力,也可以表现为支持力.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 一根长度为L的轻质直杆,两端各固定一个可视为质点的小球A和B,两球质量均为m,轻杆可以绕过其中点的水平轴在竖直平面内匀速运动.
一根长度为L的轻质直杆,两端各固定一个可视为质点的小球A和B,两球质量均为m,轻杆可以绕过其中点的水平轴在竖直平面内匀速运动.
 ,求
,求

 ,求直杆转到如图所示竖直位置时,A、B两球对直杆作用力各多大?方向如何?
,求直杆转到如图所示竖直位置时,A、B两球对直杆作用力各多大?方向如何?