题目内容
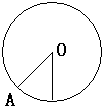 半径为R=0.8m的光滑绝缘导轨固定于竖直平面内,加上某一方向的匀强电场时,带电小球沿轨道内侧做完整的圆周运动.小球运动到A处时动能最大,A点与圆心O的连线与竖直向下方向夹一锐角,如图所示.已知小球运动到A处时对轨道的压力FN=120N,且小球运动过程中最大动能比最小动能多32J.不计空气阻力.试求:
半径为R=0.8m的光滑绝缘导轨固定于竖直平面内,加上某一方向的匀强电场时,带电小球沿轨道内侧做完整的圆周运动.小球运动到A处时动能最大,A点与圆心O的连线与竖直向下方向夹一锐角,如图所示.已知小球运动到A处时对轨道的压力FN=120N,且小球运动过程中最大动能比最小动能多32J.不计空气阻力.试求:(1)小球最小动能多大?
(2)若小球在动能最小位置时突然撤去轨道,并保持其它物理量都不变,则小球经0.04s后,其动能与原来小球运动到A处时动能相同,那么小球的质量多大?
分析:(1)小球在A处的动能最大,知A点为等效最低点,小球所受的电场力和重力的合力F方向必与OA平行,与圆心对称的点为等效最高点,动能最小,根据动能定理求出等效最高点的速度,从而得出最小动能的大小.
(2)撤去轨道后,电场力和重力的合力做功,做类平抛运动,抓住动能与原来小球运动到A处时动能相同,确定出到达的位置与A的连线与OA垂直,根据牛顿第二定律和类平抛运动的规律求出小球的质量.
(2)撤去轨道后,电场力和重力的合力做功,做类平抛运动,抓住动能与原来小球运动到A处时动能相同,确定出到达的位置与A的连线与OA垂直,根据牛顿第二定律和类平抛运动的规律求出小球的质量.
解答:解:(1)小球所受的电场力和重力的合力F方向必与OA平行,且由O指向A.
小球在A处,FN-F=m
,Ek1=
mv12
小球在A关于O点对称的圆轨道B处时动能最小,设为Ek2,则
根据动能定理得,Ek2-Ek1=-F?2R
又Ek1-Ek2=32J
联立解得F=20N,Ek2=8J.
(2)撤去轨道后小球做类平抛运动,经t=0.04s,动能与原来小球运动到A处时动能相同,因为仍然是重力和电场力做功,所以小球到达位置与A连线OA垂直.
有:F=ma,2R=
at2
由第一问求出F=20N,代入数据解得m=0.01kg.
答:(1)小球的最小动能为8J.
(2)小球的质量为0.01kg.
小球在A处,FN-F=m
| v12 |
| R |
| 1 |
| 2 |
小球在A关于O点对称的圆轨道B处时动能最小,设为Ek2,则
根据动能定理得,Ek2-Ek1=-F?2R
又Ek1-Ek2=32J
联立解得F=20N,Ek2=8J.
(2)撤去轨道后小球做类平抛运动,经t=0.04s,动能与原来小球运动到A处时动能相同,因为仍然是重力和电场力做功,所以小球到达位置与A连线OA垂直.
有:F=ma,2R=
| 1 |
| 2 |
由第一问求出F=20N,代入数据解得m=0.01kg.
答:(1)小球的最小动能为8J.
(2)小球的质量为0.01kg.
点评:本题考查了等效场问题,关键确定出圆周运动的等效最高点和最低点,结合动能定理和牛顿第二定律进行求解.

练习册系列答案
相关题目
 如图所示,一质量为m=1kg的滑块从半径为R=0.8m的光滑四分之一圆弧形槽的顶端A处无初速度地滑下,槽的底端B与水平传送带相切,传送带的运行速度恒为v=6m/s,长为L=2m,滑块滑到传送带上后做匀加速直线运动,滑到传送带末端C时,恰好被加速到与传送带的速度相同.(取g=10m/s2)
如图所示,一质量为m=1kg的滑块从半径为R=0.8m的光滑四分之一圆弧形槽的顶端A处无初速度地滑下,槽的底端B与水平传送带相切,传送带的运行速度恒为v=6m/s,长为L=2m,滑块滑到传送带上后做匀加速直线运动,滑到传送带末端C时,恰好被加速到与传送带的速度相同.(取g=10m/s2)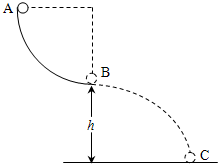 一质量为m=1kg的小球,从半径为R=0.8m的
一质量为m=1kg的小球,从半径为R=0.8m的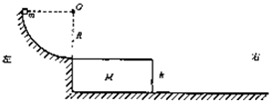 如图所示,一质量为m=1kg的小滑块从半径为R=0.8m的光滑
如图所示,一质量为m=1kg的小滑块从半径为R=0.8m的光滑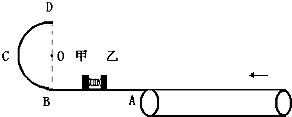 如图所示,光滑的水平面AB(足够长)与半径为R=0.8m的光滑竖直半圆轨道BCD在B点相切,D点为半圆轨道最高点.A点的右侧等高地放置着一个长为L=20m、逆时针转动速度为v0=10m/s的传送带.用轻质细线连接甲、乙两物体,中间夹一轻质弹簧,弹簧与甲乙两物体不栓接.甲的质量为m1=3kg,乙的质量为m2=1kg,甲、乙均静止在光滑的水平面上.现固定乙球,烧断细线,甲离开弹簧后进入半圆轨道并可以通过D点,且过D点时对轨道的压力恰好等于甲的重力.传送带与乙物体间摩擦因数为0.6,重力加速度g取l0m/s2,甲、乙两物体可看作质点.
如图所示,光滑的水平面AB(足够长)与半径为R=0.8m的光滑竖直半圆轨道BCD在B点相切,D点为半圆轨道最高点.A点的右侧等高地放置着一个长为L=20m、逆时针转动速度为v0=10m/s的传送带.用轻质细线连接甲、乙两物体,中间夹一轻质弹簧,弹簧与甲乙两物体不栓接.甲的质量为m1=3kg,乙的质量为m2=1kg,甲、乙均静止在光滑的水平面上.现固定乙球,烧断细线,甲离开弹簧后进入半圆轨道并可以通过D点,且过D点时对轨道的压力恰好等于甲的重力.传送带与乙物体间摩擦因数为0.6,重力加速度g取l0m/s2,甲、乙两物体可看作质点.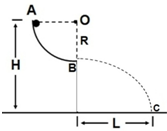 如图所示,位于竖直平面上半径为R=0.8m的1/4圆弧光滑轨道AB,A点距离地面高度为H=1m,质量为m=0.1kg的小球从A点由静止释放,通过1/4圆弧光滑轨道AB,最后落在距B点水平距离为L=4m的地面C处,不计空气阻力,g=10m/s2求:
如图所示,位于竖直平面上半径为R=0.8m的1/4圆弧光滑轨道AB,A点距离地面高度为H=1m,质量为m=0.1kg的小球从A点由静止释放,通过1/4圆弧光滑轨道AB,最后落在距B点水平距离为L=4m的地面C处,不计空气阻力,g=10m/s2求: