题目内容
如图所示，在绝缘光滑水平面的上方存在着水平方向的匀强电场，现有一个质量m=2.0×10-3kg、电量q=2.0×10-6C的带正电的物体（可视为质点），从O点开始以一定的水平初速度向右做直线运动，其位移随时间的变化规律为s=6.0t-10t 2，式中s的单位为m，t的单位为s．不计空气阻力，取g=10m/s2．（1）求匀强电场的场强大小和方向；
（2）求带电物体在0～0.5s内电势能的变化量．
分析：（1）根据位移随时间的变化规律可以得到加速度和初速度，根据牛顿第二定律即可求解；
（2）先根据匀变速运动的基本公式求解物体在0.5s内发生的位移，再求出电场力所做的功即可求解．
（2）先根据匀变速运动的基本公式求解物体在0.5s内发生的位移，再求出电场力所做的功即可求解．
解答：解：（1）由s=6.0t-10t2得加速度大小为：a=20m/s2
根据牛顿第二定律：Eq=ma
解得场强大小为：E=2.0×104N/C
电场强度方向水平向左
（2）由x=6.0t-10t2得初速度为：v0=6.0m/s
减速时间：t1=0.3s
0.3s内经过的路程x1=v0t1-a1t2=0.9 m
后0.2s物体做反向匀加速直线运动，经过的路程 x2=a2t2=0.4m
物体在0.5s内发生的位移为x=0.9-0.4=0.5
电场力做负功，电势能增加：△Ep=qEx=2×10-2J
答：（1）求匀强电场的场强大小为2.0×104N/C，方向水平向左；
（2）带电物体在0～0.5s内电势能的变化量为2×10-2J．
根据牛顿第二定律：Eq=ma
解得场强大小为：E=2.0×104N/C
电场强度方向水平向左
（2）由x=6.0t-10t2得初速度为：v0=6.0m/s
减速时间：t1=0.3s
0.3s内经过的路程x1=v0t1-a1t2=0.9 m
后0.2s物体做反向匀加速直线运动，经过的路程 x2=a2t2=0.4m
物体在0.5s内发生的位移为x=0.9-0.4=0.5
电场力做负功，电势能增加：△Ep=qEx=2×10-2J
答：（1）求匀强电场的场强大小为2.0×104N/C，方向水平向左；
（2）带电物体在0～0.5s内电势能的变化量为2×10-2J．
点评：本题是多过程问题，关键是理清物体在整个过程中的运动情况，结合牛顿第二定律及运动学公式进行求解．
练习册系列答案
相关题目
如图所示，在绝缘光滑水平面上，有一个边长为L的单匝正方形线框abcd，在外力的作用下以恒定的速率v向右运动进入磁感应强度为B的有界匀强磁场区域．线框被全部拉入磁场的过程中线框平面保持与磁场方向垂直，线框的ab边始终平行于磁场的边界．已知线框的四个边的电阻值相等，均为R．求：
如图所示，在绝缘光滑的水平面上固定两个带有等量同种电荷的小球P、Q，在PQ之间的M点由静止释放一带电滑块，则滑块会由静止开始向右运动到PQ之间的另一点N而速度减为零，在此过程中，以下说法正确的是（ ）
如图所示，在绝缘光滑水平面上，可视为质点的A、B两个带正电的小球相距为r，带电量分别为4q和q．B的质量为m，在库仑力作用下，两球从静止开始运动：起初，A的加速度大小为a、B的加速度大小为4a；经过一段时间后，B的加速度大小为a，速度达到v．试计算这时：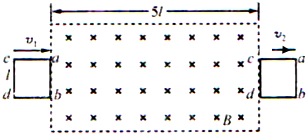
如图所示，在绝缘光滑的水平面上，有一个质量为m、边长为L的正方形线框，用一垂直于ab 边的恒定外力将正方形线框以速率v1匀速拉进磁感应强度为B的有界匀强磁场区域，当正方形线框全部进入磁场后立即将外力撤去，线框最终能完全离开磁场，若测得cd边刚要离开磁场时速率为v2，已知磁场方向竖直向下，宽度为5L，正方形线框每条边的电阻均为R，求：
（2011?浙江模拟）如图所示，在绝缘光滑的水平面上固定两个电量相等的异种点电荷A、B，其中A带正电，B带负电荷，它们的连线的中点是O，MN是AB在水平面内中垂线上的两点．空间中还有一个垂直于该水平面的磁场（图中未画出）．现有一个带电量为+q的小球以初速度v0从M点沿MN方向射入，恰能沿中垂线由M点向N点运动，则下列说法中正确的是（ ）