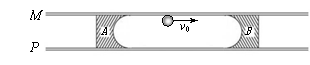
��Ŀ����
�̶���ˮƽ���ϵ�����������ֱ����MN��PQ���ڲ��������߸�������ȫ��ͬ����A��B������İ��۰뾶��R������Ŀ���Ϊ2R���ȵ�������С������������ص��컬�У���ͼ��ʾ������һ��Ħ�������а뾶r��r����R���Ľ���С����ˮƽ���ٶ�v0�����һ��飬�ӻ����һ���Բ�βۿڱ�Ե���룮��֪����С�������Ϊm��A��B�����������Ϊkm������k=1��2��3���������˶���������е����ʧ����

��1��������С���һ�λ���B����ʱ������С����ٶ��Ƕ��
��2����С���B������������ײ2�Σ���k��ȡֵ��Χ��

��1��������С���һ�λ���B����ʱ������С����ٶ��Ƕ��
��2����С���B������������ײ2�Σ���k��ȡֵ��Χ��
��������1������С����B�������ã����ݶ����غ�ͻ�е���غ���
��2������С����A�������ã����ݶ����غ�ͻ�е���غ��г���ʽ������С��ͻ�����˶�����жϣ�
��2������С����A�������ã����ݶ����غ�ͻ�е���غ��г���ʽ������С��ͻ�����˶�����жϣ�
����⣺��1���軬��B����ʱ��С���B������ٶȷֱ�Ϊv1��v2��
�ɶ����غ�ɵ�mv0=mv1+kmv2
�ɻ�е���غ�ɵ�
m
=
m
+
km
�������С���ٶ�Ϊv1=
v0
B�����ٶ�Ϊv2=
v0
��2���軬��A����ʱ��С���A������ٶȷֱ�Ϊv1����v2����
�ɶ����غ�ɵ�mv1=mv1��+kmv2��
�ɻ�е���غ�ɵ�
m
=
mv
+
kmv
�������С����ٶ�
=
v1=(
)2v0
��С���B������������ײ2�Σ������|
|��
����k2-4k-1��0
���K��2+
��k=5��6��7
�𣺣�1��������С���һ�λ���B����ʱ������С����ٶ���v1=
v0
��2����С���B������������ײ2�Σ�k=5��6��7
�ɶ����غ�ɵ�mv0=mv1+kmv2
�ɻ�е���غ�ɵ�
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
�������С���ٶ�Ϊv1=
| 1-k |
| 1+k |
B�����ٶ�Ϊv2=
| 2 |
| 1+k |
��2���軬��A����ʱ��С���A������ٶȷֱ�Ϊv1����v2����
�ɶ����غ�ɵ�mv1=mv1��+kmv2��
�ɻ�е���غ�ɵ�
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| �� | 2 1 |
| 1 |
| 2 |
| �� | 2 2 |
�������С����ٶ�
| v | / 1 |
| 1-k |
| 1+k |
| 1-k |
| 1+k |
��С���B������������ײ2�Σ������|
| v | �� 1 |
| v | 2 |
����k2-4k-1��0
���K��2+
| 5 |
��k=5��6��7
�𣺣�1��������С���һ�λ���B����ʱ������С����ٶ���v1=
| 1-k |
| 1+k |
��2����С���B������������ײ2�Σ�k=5��6��7
���������⿼���˶������������ۺ����⣬������������ע��ѡȡ�о��������˶����̣�������Ӧ������⣮

��ϰ��ϵ�д�
�����Ŀ