题目内容
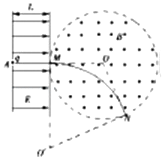
【题目】如图所示,空间分布着方向平行于纸面且与场区边界垂直的有界匀强电场,电场强度为E、场区宽度为L.在紧靠电场右侧的圆形区域内,分布着垂直于纸面向外的匀强磁场,磁感应强度B大小未知,圆形磁场区域半径为r.一质量为m,电荷量为q的带正电的粒子从A点由静止释放后,在M点离开电场,并沿半径方向射入磁场区域,然后从N点射出,O为圆心,∠MON=120°,粒子重力可忽略不计.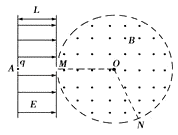
(1)求粒子经电场加速后,进入磁场时速度的大小;
(2)求匀强磁场的磁感应强度B的大小及粒子从A点出发到从N点离开磁场所经历的时间;
(3)若粒子在离开磁场前某时刻,磁感应强度方向不变,大小突然变为B′,此后粒子恰好被束缚在磁场中,则B′的最小值为多少?
【答案】
(1)解:设粒子经电场加速后的速度为v,根据动能定理有:
EqL= ![]() mv2
mv2
解得:v= ![]()
答:粒子经电场加速后,进入磁场时速度的大小v= ![]() ;
;
(2)解:粒子在磁场中完成了如图所示的部分远运动,设其半径为R,因洛伦兹力提供向心力所以有:
qvR=m ![]()
由几何关系得: ![]() =tan30°
=tan30°
所以B= ![]()
设粒子在电场中加速的时间为t1,在磁场中偏转的时间t2
粒子在电场中运动的时间t2= ![]() m=
m= ![]()
粒子在磁场中做匀速圆周运动,其周期为T= ![]() =
= ![]()
由于∠MON=120°,所以∠MO′N=60°
故粒子在磁场中运动时间t2= ![]() T=
T= ![]()
所以粒子从A点出发到从N点离开磁场所用经历的时间:
t=t1+t2= ![]() +
+ ![]()
答:匀强磁场的磁感应强度B的大小及粒子从A点出发到从N点离开磁场所经历的时间 ![]() +
+ ![]() ;
;
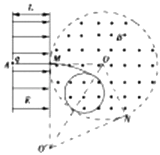
(3)解:如图所示,当粒子运动到轨迹与OO′连线交点处改变磁场大小时,粒子运动的半径最大,即B′对应最小值,
由几何关系得此时最大半径有:Rm= ![]()
所以B′=( ![]() +1)
+1) ![]()
答:若粒子在离开磁场前某时刻,磁感应强度方向不变,大小突然变为B′,此后粒子恰好被束缚在磁场中,则B′的最小值为( ![]() +1)
+1) ![]() .
.
【解析】(1)设粒子经电场加速后的速度为v,根据动能定理即可求解v;(2)根据洛仑兹力提供向心力及几何关系即可求解粒子在磁场中运动的周期,进而得到磁场中的运动时间与粒子从A点出发到从N点离开磁场所用经历的时间;(3)粒子在电场中做匀加速,在磁场中做圆周运动,根据匀加速直线运动时间位移公式和圆周运动的周期公式即可解题.
【考点精析】根据题目的已知条件,利用带电微粒(计重力)在电场中的运动的相关知识可以得到问题的答案,需要掌握带电颗粒:如液滴、油滴、尘埃、小球等,除有说明或明确的暗示以外,一般都不能忽略重力;由于带电粒子在匀强电场中所受电场力与重力都是恒力,因此可以用两种方法处理:①正交分解法;②等效“重力”法.

 阅读快车系列答案
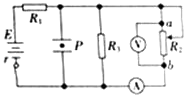
阅读快车系列答案【题目】在测量电源的电动势和内阻的实验中,由于所用的电压表(视为理想电压表)的量程较小,某同学设计了如图所示的实物电路.
(1)实验时,应先将电阻箱的电阻调到 . (选填“最大值”、“最小值”或“任意值”)
(2)改变电阻箱的阻值R,分别测出阻值R0=10Ω的定值电阻两端的电压U,下列两组R的取值方案中,比较合理的方案是 . (选填“1”或“2”)
方案编号 | 电阻箱的阻值R/Ω | ||||
1 | 400.0 | 350.0 | 300.0 | 250.0 | 200.0 |
2 | 80.0 | 70.0 | 60.0 | 50.0 | 40.0 |
(3)根据实验数据描点,绘出的 ![]() 图象是一条直线.若直线的斜率为k,在
图象是一条直线.若直线的斜率为k,在 ![]() 坐标轴上的截距为b,则该电源的电动势E= , 内阻r= . (用k、b和R0表示)
坐标轴上的截距为b,则该电源的电动势E= , 内阻r= . (用k、b和R0表示)